Считаем вероятности

Добрый день, дорогие читатели!

Продолжаем делать добрые дела вместе с вами:
- в августе прошлого года вы исправили статью википедии, содержавшую явный бред по поводу задачи о двух конвертах,
- на этой неделе, разбираясь с сектантами на острове Беззеркалья, вы исправили другую статью википедии. И это тоже добавило адекватности всемирной энциклопедии (жаль, что ту статью пока никто не перевёл на русский язык).

Но можно ли на этом остановиться? Увы, плюсы открытой википедии часто становятся её минусами: любой человек, не разбирающийся в предмете, может внести в неё что угодно. И это делается не со зла, а из-за искренней убеждённости в своей правоте (логические парадоксы умеют перетягивать в неправильную сторону). А понимающим людям часто даже не приходит в голову читать подобные статьи, поэтому ошибки такого типа копятся (а потом тиражируются, например, журналистами).

В наш век быстрого распространения бреда информации есть два варианта: уметь фильтровать откровенную ложь или слепо следовать за красивыми словами тех, кто даже не понимает своей собственной позиции.

На мой взгляд, разбор логических, геометрических и вероятностных задач очень полезен. Дело в том, что человек, разобравшийся с подобным решением, уже не так легко верит на слово красивым высказываниям о вероятностях и математических ожиданиях, не покупается на цветные графики и чертежи. А это несколько ограничивает влияние манипуляторов на действия большинства.

Поэтому сегодня я предлагаю вернуться к парадоксу двух конвертов, чтобы разобрать один частный случай. Я уверен, что многие из вас сами могли найти, понять и исправить ту ошибку. Но уже несколько месяцев она висит в статье википедии, поэтому я предлагаю в неё вникнуть чуть подробнее.

Коротко напомню постановку задачи: есть два конверта, в одном из которых находится сумма вдвое большая, чем в другом. Игрок выбирает один конверт, пересчитывает в нём деньги, а после этого решает, оставить его себе, или взять другой.

Интуиция подсказывает, что если в первом вытянутом конверте находится X денег, то во втором с раными вероятностями будет X/2 и 2X. В прошлом году мы разобрались с этим заблуждением. Но до сих пор поступают комментарии от людей, которые не очень уверенно умеют рассчитывать вероятности сумм во втором конверте для частных случаев.

Да и в упомянутой статье википедии содержатся неверные выкладки. Цитата: «Например, если предположить, что сумма в меньшем конверте равномерно распределена между 10 руб. и 100 руб., очевидно такое:
* Если выпало 15 руб., в другом конверте определённо 30 руб. (7,5 быть не может). Поэтому требуется брать другой конверт.
* Если выпало 25 руб., в другом может быть как 12,5 руб., так и 50 руб., но вероятность второго больше — желательно брать другой конверт.
* Если выпало 90 руб., в другом может быть как 45 руб., так и 180 руб., при этом больше вероятность первого — лучше не брать другой конверт.
* Если выпало 100 руб., в другом конверте определённо 50 рублей — ни в коем случае не брать другой конверт».

Вам тоже кажется, что последние три пункта как минимум странные? И то, что они предваряются словами, «очевидно такое», никак не улучшает ситуации.

Давайте честно рассчитаем вероятности! В меньшем конверте находится случайное число от 10 до 100, поэтому в большем - от 20 до 200. Это значит, что вытянув конверт, мы можем получить какое-то число от 10 до 200. Давайте разделим этот интервал на три части:
1) 10 <= X < 20,
2) 20 <= X <= 100,
3) 100 < X <= 200.

Чем хороши первый и третий диапазоны? Тем, что попав в них (не важно с какой вероятностью), мы точно знаем, сумма в нашем конверте X является большей из двух сумм в конвертах или меньшей. Это значит, что если X<20 или если X>100, то мы на 100% уверены, что делать.

Осталось разобраться со средним диапазоном. Давайте поймём, как формируются конверты:
- кто-то умеет генерировать случайные величины Y от 10 до 100, равномерно распределяя числа в этом диапазоне,
- кто-то другой берёт эти числа, чтобы сформировать пару для конверта (Y, 2Y) - это наши равновероятные элементарные исходы,
- мы (игрок) вытягиваем число X, открыв случайный из этих двух конвертов.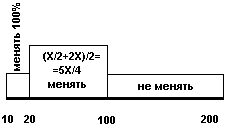

И как же было получено это число X? Очень просто - оно оказалось большим или меньшим в сгенерированной паре (Y, 2Y). Другими словами, нам досталась одна из пар (X, 2X) или (X/2, X). А мы вытянули из неё число X.

Но мы же знаем, что меньшее число в этих парах - случайная величина, имеющая равномерное распределение на диапазоне от 10 до 100. Это означает, что все пары (Y, 2Y) появляются с равными вероятностями. И из этого следует, что вероятности генерации пар (X, 2X) и (X/2, X) одинаковы, так? Поэтому, если уж нам досталось число X от 20 до 100, то вероятности того, что во втором конверте будет 2X или X/2 равны, верно?

Поэтому «правильный» вывод состоит в следующем:
- Если вытянутое число больше 100, то менять конверт не следует, так как это гарантированно приведёт к уменьшению выигрыша,
- Если вытянутое число меньше 20, то обязательно надо сменить конверт, так как это гарантирует увеличение выигрыша,
- В остальных случаях тоже стоит сменить конверт, так как вероятность удвоения суммы равна вероятности её сокращения в два раза, но возможный выигрыш при замене больше возможного проигрыша.

Всё это очень просто и для дискретного случая (когда в конвертах могут быть только целые числа, например). Только тогда придётся вникать в чётность (так как нечётный X однозначно указывает на то, что следует поменять конверт), а это сделает решение чуть более громоздким.

Хорошего вам дня и интересного чтения энциклопедий!

P.S.
кстати, кто заметил ошибку в рассуждениях выше? ;)

Дополнение: пояснения даны в следующей заметке.