Напальцы, основы электричества, психология для детей

Добрый день!

1) Если вы тоже с удовольствием читали «объяснения на пальцах», то это видео для вас.

Здесь научно-популярный Youtube-канал о космосе Alpha Centauri здорово начал с переработки статьи «Как измерить скорость света? На Пальцах» (естественно, согласовав с автором):


https://youtu.be/DZ6U1XBLCiA

Мне заранее было понятно, что тут отличный текст, также я ожидал хороший видеоряд, но, извините, по-настоящему впечатлило правильное склонение числительных! Мало где сейчас это умеют :)

2) Несколько лет назад вы могли познакомиться с переводом первого тома интересной книги «Экспериментальные и Исторические Основы Электричества» (кстати, перевод выполнил извенстный многим по комментариям здесь Артур Бараов), а сейчас появился и второй том этого труда.

Стоит ли обратить внимание на эту книгу? По-моему, да, ведь она ярко показывает, как важны эксперименты для понимания физики. Кроме того, по словам Артура, перевод этой книги помог и ему продвинуться в исследованиях (см. пример).

3) А теперь вопрос: какие хорошие детские книги по психологии вы знаете? Увы, в ранее совместно собранной коллекции хороших книг и в её продолжении про психологию для детей практически ничего нет.

Возможно, это совсем редкий или неправильный жанр? В сети я нашёл положительные отзывы на книгу «Мой первый учебник по психологии: Книга для подростка» Владислава Яровицкого, но саму книгу пока нигде добыть не смог (чем лучше книга, тем меньше тираж обычно, но обратно верно далеко не всегда, к сожалению). Сможете вспомнить, после прочтения какой книги об устройстве себя и окружающих ребёнок обрадовался?

Хороших выходных!

Экспериментальные и исторические основы электричества

Добрый день!

Прочитать или услышать о том, как устроен мир по мнению учёных — это полезно. Но своими руками и мозгами открыть закономерности — гораздо интереснее и потому эффективнее!

Если исходить из того, что наука — это лучший способ удовлетворения личного любопытства за государственный счёт, то становится понятнее, как готовить будущих великих учёных или хотя бы крепких специалистов. Их надо не только заставлять запоминать то, что им не очень-то интересно, но и давать возможность исследовать новое, аккуратно направляя эти исследования в полезную и безопасную сторону.

Поэтому спешу с вами поделиться книгой «Экспериментальные и Исторические Основы Электричества», перевод которой выполнил знакомый многим по комментариям Артур Бараов. С этой книгой ребёнок сможет работать и самостоятельно, но мне кажется, что делать опыты совместно с родителями — это самый эффективный режим.

В комментариях к этой заметке приглашаю делиться ссылками на полезные для детского развития книги (если можно, указывайте, пожалуйста, рекомендуемый возраст читателя, область знаний и небольшой комментарий). Примерно так:
- «Книга о самых невообразимых животных» (Хендерсон, Каспар), биология, вызывает интерес уже с 5-7 лет, на странных и неожиданных примерах демонстрирует основные понятия, тем самым расширяя кругозор читателя.

(Цель прежняя — продолжить собирать коллекцию книг, полезных для развития маленьких и взрослых)

Хорошего дня!

Записи опытов и способы увлечь наукой

Здравствуйте.

Несколько лет назад я рассказывал, какие бывают способы улучшить климат в квартире, а недавно автор познавательных технических обзоров Артамонов Олег интересно рассказал о том, как он решает эту задачу. Рекомендую пару его статей о том, «Какой увлажнитель выбрать?» и «Зачем увлажнитель нужен?»

А теперь к главному: последние годы всё больше людей понимают, что youtube можно использовать не только для просмотра развлекательных роликов. Многие догадываются, что можно снимать хорошие уроки на видео, чтобы заинтересовать детей наукой и даже чтобы чему-то научить. В этой заметке мы попробуем собрать коллекцию ссылок на путные ресурсы, посвящённые этому делу. Пожалуйста, оставьте комментарий со своими любимыми сайтами!

Приведу пример из математики, который мне попался только что (конечно, это не столько популяризаторский ролик, сколько демонстрация забавного популяризаторского устройства): «Генератор простых чисел».

А что ещё мы знаем хорошего о попытках дистанционного обучения на русском языке? У меня есть такой список:

- Огромный lektorium.tv — это первое, что пришло в голову. Что значит огромный? На странице со списком лекторов перечислено около тысячи фамилий! Работа проделана огромная, найти можно многое, темы есть самые разные, классификатор удобный, взрослому человеку оторваться трудно, но ребёнка проект едва ли увлечёт, к сожалению.

- У «Научной России» опубликовано мало лекций, причём у меня сложилось впечатление, что все они есть на lektorium.tv. Но там неплохой поток интересных новостей! Некоторые вещи на сайте не очень удобны: отсутствует сортировка по алфавиту в списке рубрик (несколько раз мозг терялся, когда надо было быстро найти, например, «математику»), рядом с тэгом не указано количество элементов, имеющих этот же тэг (это мешает быстро искать материалы по близким темам, так как приходится тратить время на просмотр списков из той единственной статьи, которую я и так уже прочитал). Учиться здесь не получится, но расширить кругозор можно — старшие школьники могут заинтересоваться и подписаться.

- На «Элементах» всегда есть, что прочитать и посмотреть. Например, раздел видеотека содержит много интересных и качественных материалов для школьников. Весьма полезен раздел «Лекции и мастер-классы для учителей» (кстати, такие ролики иногда оказываются детям даже более интересными, чем специально для них приготовленные «завлекалочки»; школьник, задумавшийся о том, как правильнее его учить — это здорово!). Сам сайт очень большой и разноплановый, поэтому приличному школьнику его стоит регулярно посещать.

- Сайт «Простая наука» попадался мне несколько раз, с завлечением детей там дела обстоят неплохо, но я не увидел, «что дальше?» (т.е. что смотреть ребёнку, если он заинтересовался физикой или химией?), а также не нашёл удобного способа оглядеть, что есть ещё (деление роликов на темы достаточно грубое, хорошего способа искать что-либо я не обнаружил). Кроме того, иногда опыты поставлены не очень корректно (не так плохо, как у «Разрушителей легенд», но глаз всё же режет), но это всё на мой взгляд математика.

- Сайт getaclass.ru очень маленький (пара десятков роликов), содержит материалы только по начальной физике, но кажется очень продуманным: в коротких роликах демонстрируется опыт и его объяснение, а также разбираются задачи по пройденной теме. Взрослому человеку смотреть интересно, а школьнику должно быть ещё и полезно. Задача увлечь наукой выполнена умеренно, но это компенсируется познавательностью роликов.

- Особняком стоит naukatv.ru — написано там всё заманчиво, но увидеть мне пока ничего не удалось. Телевизионный формат образовательных передач я не очень понимаю, потому что без возможности нажимать паузу и перематывать воспринимать новое знание должно быть тяжело.

- Есть ещё небольшие, но, как я понимаю, с любовью составленные подборки:
-- статья «Занимательные опыты по физике» в Первом сентября,
-- «Занимательная физика» (пять роликов и ряд текстов),
-- «Уроки волшебства» (описание ряда опытов).

Этот список можно составлять долго, рунет большой. А оценивать, что из этого хорошо, можно ещё дольше. Поэтому я прошу вас продолжить традицию заметки «Что читать?» — напишите, пожалуйста, что стоит показать ребёнку, чтобы заинтересовать его наукой. Зачем? Чтобы увлечённее учился! Ведь только так можно учиться эффективно.

Хорошего дня!

Разноцветные шляпы и бозон Хиггса

Добрый день.

Опять мы можем наблюдать, как на этот блог с поисковых систем приходят десятки людей по запросу «27 августа в 00:30, подними глаза и посмотри на ночное небо. В эту ночь планета Марс, пройдет всего лишь в 34,65 тыс. милях от земли». Это означает, что уже середина июля, поэтому половина лета уже почти прошла.

Кстати, если вам тоже очевидна физическая глупость текста из приведённой выше цитаты (про грамотность промолчу), то, возможно, заметка «Что такое бозон Хиггса» как раз для вас. В ней автор кратко и весьма доступно рассказывает, в чём был смысл исследования, результаты которого недавно обнародовали учёные, работающие на большом адронном коллайдере, какие статистические вопросы возникают при анализе результатов детекторов, как дальше жить физикам и так далее. В тексте есть реверансы на тему «на самом деле всё не так», но на то это и передний край науки спереди, чтобы не иметь даже надежды узнать точно, как устроен мир.

Теперь вернёмся к математике: задачу про 100 мудрецов в колонне, мы неплохо порешали, поэтому можно осмотреться, что ещё бывает в этой области:

- задача про 99 мудрецов и два цвета:
99 мудрецов сели за круглый стол. Им известно, что пятидесяти из них надели колпаки одного из двух цветов, а сорока девяти остальным — другого. Все мудрецы должны одновременно сообщить (написать на бумажке) цвет своего колпака. Для какого наибольшего значения k можно гарантировать, что не менее k мудрецов могут сделать это правильно? (Разумеется, мудрецы могут заранее — до надевания колпаков — выработать совместно используемую стратегию) Осторожнее переходите по ссылке выше, так как там есть ответ и решения!

- задача про бесконечное количество мудрецов (сложная, парадоксальная, но полезная). Текст здесь не привожу, но любителям прекрасного рекомендую ознакомиться с условием.

Первая задача интересна тем, что правильный ответ многие могут почувствовать, а вот для оформления честного решения требуются гораздо большие усилия. Вторая же задача является ещё более чудесным поводом помассировать мозг.

Благодарю всех, кто нашёл время поделиться информацией о хороших книгах. Похоже, формулировка «это такая хорошая книга, которую мало кратко похвалить, а следует посвятить ей подробную, качественную и продуманную рецензию, чем я и займусь, как только найду чуть-чуть времени» объясняет небольшое количество рекомендаций. Поэтому я призываю: забудьте про совершенство формы, поделитесь содержанием!

Хорошего дня!

Найдите отличия

Что-то увлеклись мы физикой (уже более 80 комментариев в обсуждении задачки про два автомобиля), поэтому сейчас будет простой математический вопрос, который мог бы быть в давнем ЕГЭ, а потом... опять физика :)

Итак, дана функция у = f(x). На каком из промежутков эта функция возрастает?
1) (-∞, 5];
2) [-2, 4];
3) (2, 3);
4) (0, 8).
Думаете я забыл добавить картинку к заметке? ;)

А теперь возвращаемся к физике (эту задачку предложил обсудить один из читателей).

Объясните отсутствие нарушения закона сохранения энергии в следующем случае:
Дан конденсатор ёмкости C с зарядом 2Q. Его энергия равна (2Q)^2/2C. Параллельно ему мы подключили пустой конденсатор такой же ёмкости, после чего заряд равномерно распределился по этим двум конденсаторам. По идее (по формулам) общая энергия этой системы стала Q^2/2C+Q^2/2C = Q^2/C (т.е. в 2 раза меньше, чем изначальная). Но по здравой логике энергия никуда не должна исчезать (заряды-то никуда не делись, как был суммарный 2Q, так и остался).

Многие не любят задачки про электричество, потому что в школе редко хорошо проходят эту тему. Поэтому давайте переведём это же условие на язык жидкостей (такая аналогия часто оказывается не только полностью корректной, но и гораздо более ясной, так как с жидкостями-то мы привыкли иметь дело).

Объясните отсутствие нарушения закона сохранения энергии в следующем случае:
Дана вертикальная цилиндрическая бочка с водой (высота бочки 2h, масса воды 2m). Потенциальная энергия воды в поле тяжести равна 2mgh. Рядом ставим пустую бочку такой же формы, соеденив её с первой бочкой трубочкой, после чего вода равномерно распределился по этим двум бочкам. По идее (по формулам) общая энергия этой системы стала mgh/2+mgh/2 = mgh (т.е. в 2 раза меньше, чем изначальная). Но по здравой логике энергия никуда не должна исчезать (вода-то никуда не делась, как была суммарная масса 2m, так и осталась).

Кстати, водная аналогия позволяет лучше понять вот какую вещь: если трубочка, соединяющая бочки, будет толстой, то половина воды быстро перетечёт во вторую ёмкость (если сопротивление проводника между конденсаторами будет малым, то заряд быстро перераспределится). Но эта толщина трубочки (сопротивление проводника) не влияют на финальное количество энергии.

В чём вопрос? Как обычно:
0) На каком из промежутков возрастает функция f(x) из начала заметки?
1) Объясните отсутствие нарушения закона сохранения энергии в обоих случаях.
2) Чем так отличаются примеры с водой и электричеством, что про бочку воды мы не сомневаемся, а с конденсаторами есть ощущение, что что-то не так?

Хорошего дня!

Как решать задачу по физике?

А сегодня мы попробуем хорошо ответить на вопрос про два автомобиля и сохранение энергии. Напомню, что мы играем в устное собеседование, мы примерно понимаем цели этого мероприятия, поэтому даже догадываемся, как отвечать на собеседовании, значит осталась мелочь. Давайте вспомним саму задачку:

Два автомобиля массы m едут со скоростью v по дороге в одну сторону. В системе отсчёта дороги их кинетическая энергия равна mv²/2. А относительно друг друга их скорость равна нулю, поэтому и кинетическая энергия рава нулю. Теперь один из автомобилей потратил литр бензина, чтобы разогнаться до скорости 2v. Его кинетическая энергия в лабораторной системе отсчёта стала равной m(2v)²/2 = 2mv². А в системе отсчёта второго автомобиля его кинетическая энергия стала mv²/2 (так как их скорости отличаются на v). Возникает вопрос: почему сжигание одинакового количества топлива в разных системах отсчёта привело к отличающемуся в три раза приросту энергии объектов? Закон сохранения энергии ведь никто не отменял.

Для начала перечислим, чего говорить не надо:
- «А в чём проблема? Ну и пусть отличается в три раза, что такого-то?»
- «Нет здесь никакого парадокса! Физическая теория работает в куда более сложных случаях. И здесь всё правильно поэтому».

Надо понимать, что экзаменатор, который предложил эту задачку, знает физику и много раз уже слышал размышления об этих двух автомобилях. Поэтому лучше не терять время на пустые слова, а понять, чего он хочет. А хочет он убедиться, что у кандидата есть вменяемые представления о законе сохранения энергии, развита способность внятно излагать и так далее (эта задачка хороша тем, что даёт поводы для многих дополнительных вопросов, если собеседующему захочется углубиться в каких-то направлениях).

Итак, сначала надо объяснить, почему кажется, что есть парадокс: «В самом деле, в разных системах отсчёта было извлечено одинаковое количество энергии из горючего, поэтому может казаться, что и прирост энергии в разных системах должен быть равным. Ошибка именно в этом месте, так как почему-то совершенно не рассмотрена работа внешних сил, которая в разных системах будет отличаться».

Вообще говоря, услышав такие слова, экзаменатор может решить, что дальше можно и не разговаривать, так как, скорее всего, соискатель всё прекрасно понимает. Очень может быть, что после этого будет предложена более интересная задачка. Впрочем, и в этой можно поразбираться, так как возможностей для дополнительных вопросов она даёт массу.

Поэтому давайте продолжим: «Убедимся, что работа внешних сил в разных системах отсчёта тоже отличается в три раза (как и приросты кинетических энергий). Для начала рассмотрим частный случай - равноускоренное движение разгоняющегося автомобиля. Пусть разгон происходит за время t (естественно, одинаковое в разных система отсчёта).

В лабораторной системе отсчёта автомобиль разогнался со скорости v до 2v. При этом он прошёл расстояние 3vt/2 (так как ускорение постоянное). Это значит, что совершена работа 3Fvt/2. А в системе отсчёта равномерно двигающегося автомобиля разгон произошёл с нулевой скорости до v, поэтому расстояние пройдено меньшее - vt/2, а значит, работа тоже меньше - Fvt/2. Что и требовалось понять».

Если и в этот момент собеседующий не остановит, то можно попробовать развить мысль, насколько это возможно без бумажки: «Для частного случая равноускоренного движения мы всё поняли, но этого, конечно, недостаточно. Давайте разберёмся с общим случаем - разгоном автомобиля с непостоянным ускорением.

В этом случае рассуждения можно повторить, если воспользоваться формулой dE=v*dP (изменение энергии равно произведению скорости на изменение импульса). Достаточно проинтегрировать обе части этого равенства по интервалам импульсов в разных системах отсчёта».

Кстати, в этот момент нас уже могут спросить, что это за формула и почему мы можем ею пользоваться. Поэтому давайте её быстренько докажем: «dP = F(t)dt, а dx = v(t)dt, поэтому dx = v(t)dP/F(t). А изменение энергии dE = F(t)dx = v(t)dP» (такие вещи уже нелегко делать в уме, поэтому нам, если уже задали такой дополнительный вопрос, то предложат доску и маркер или бумажку и ручку). Главное - не растеряться, а спокойно всё вывести, продемонстрировав знание определений и умение производить простейшие преобразования.

Раз уж мы зашли так далеко, то давайте добьём задачку: «В таком подходе мы можем манипулировать непосредственно скоростями и импульсами, а не координатами и временем, что позволяет нам не обращать внимание на величину мгновенного ускорения.

Изменение энергии равно работе A, которая равна интегралу от VdP по интервалу от P1 до P2, который равен интегралу от PdP/m (по тому же интервалу), который равен разнице квадратов импульсов P1 и P2, делённой на 2m. Если подставить значения начального и конечного импульсов, то эта формула повторит уже известный результат - изменение энергии в лабораторной системе отсчета будет в 3 раза больше».

Как это всё почувствовать? Представьте себе беговую дорожку, двигающуюся со скоростью v. По ней едут два автомобиля (тоже со скоростью v относительно поверхности дорожки). Относительно планеты оба автомобиля стоят на месте. Теперь один из них начинает ускоряться до скорости 2v (относительно ленты). Заметьте, что расстояние относительно планеты (или второго автомобиля), которое пройдёт разгоняющийся автомобиль, пока достигнет удвоенной скорости, гораздо меньше, чем расстояние, которое он проехал вдоль движущейся ему навстречу ленты. Как мы уже знаем, эти расстояния как раз различаются в три раза. Какой-то такой образ тоже вполне подходит для объяснения этой задачки, конечно, если не шибко путаться. Главное - объяснить, что происходит. Если подкрепить объяснения выкладками, то это будет хорошо. Но даже внятное пояснение на пальцах, показывающее незамутнённость - это уже очень ценно.

Я дополнил текст заметки «Устные задачки» ссылками на все три разбора (включая этот), поэтому сейчас, я думаю, та заметка вполне подходит, чтобы рекомендовать её идущим на собеседования. Если у вас есть такие знакомые, то покажите им её. Надеюсь, это увеличит их шансы попасть на желанную учёбу или работу. Успехов!

Устные задачки

Добрый день.

Чем отличается письменный экзамен от устного? Одно из важных различий состоит в том, что при формировании письменной работы мы не имеем обратной связи с проверяющим, а на устном вполне можно успеть себя поправить, если «чуть-чуть» пойти не в ту сторону.

Опять же, экзаменатору удобен устный опрос, потому что не приходится сомневаться, написана эта конкретная глупость по невнимательности или по незнанию, так как можно проверяемого переспросить (это если нам умные важнее внимательных, например).

Есть у устных собеседований и недостатки:
- медленные люди на них оказываются в невыгодной ситуации, так как не успевают сообразить, что требуется в простой ситуации (хотя эти же люди способны справиться со сложным вопросом, если им дать достаточно времени),
- больший простор для проявления субъективности (на мнение оценивающего начинают влиять внешность и манера говорить собеседуемого, из-за чего снижается вес знаний),
- так как на устном экзамене невозможно задать сложный вопрос, экзаменатору приходится искать простые и интересные формулировки (а их значительно меньше, чем сложных и интересных). Из-за этого собеседование иногда превращается в проверку, видел ли опрашиваемый раньше этот вопрос и ответ на него, а должно всё-таки проверяться его умение самостоятельно справиться с вопросом.

Впрочем, есть ситуации, когда это всё не является проблемой - если мы проводим отбор быстрых и приятных в общении людей, имеющих широкий кругозор и большой опыт решения различных задач.

Предлагаю три задачки из разных областей знаний: геометрия, арифметика и физика. Если захочется потянуться к карандашу и бумаге, то остановите себя, так как это устные задачки. Здесь не надо рисовать и выписывать формулы, а достаточно всего лишь показать свою способность разбираться с простыми вопросами, запоминать совсем небольшие объёмы данных, делать верные логические переходы и так далее.

1. Через середины трёх рёбер куба провели два отрезка (как на рисунке). Найдите угол между этими отрезками.

2. Найдите наименьшее натуральное n, такое, что n-я степень натурального числа не бывает шестизначным числом (задачка из ЖЖ Константина Кнопа, но будьте осторожны, нажимая на ссылку, так как там опубликован ответ).

3. Два автомобиля массы m едут со скоростью v по дороге в одну сторону. В системе отсчёта дороги их кинетическая энергия равна mv²/2. А относительно друг друга их скорость равна нулю, поэтому и кинетическая энергия рава нулю. Теперь один из автомобилей потратил литр бензина, чтобы разогнаться до скорости 2v. Его кинетическая энергия в лабораторной системе отсчёта стала равной m(2v)²/2 = 2mv². А в системе отсчёта второго автомобиля его кинетическая энергия стала mv²/2 (так как их скорости отличаются на v). Возникает вопрос: почему сжигание одинакового количества топлива в разных системах отсчёта привело к отличающемуся в три раза приросту энергии объектов? Закон сохранения энергии ведь никто не отменял.

Кстати, год назад мы рассматривали одну задачку о сохранении энергии - и вот её разбор.

Дополнение. Ниже перечислены заметки, имеющие отношения к данной:
Как отвечать на собеседовании?
Как решать задачку по геометрии?
Как решать задачку по алгебре?
Как решать физическую задачку?

Хорошего дня!

Физика для всех возрастов

Сегодня в нашей рубрике «Три чего-нибудь» мы будем искать тех, кому можно не просто задать вопрос «Почему небо голубое?», но и получить внятный ответ.

1) Начнём со зрелого возраста. С 1918 года журнал «Успехи физических наук» систематически открывает всем желающим глаза на передний край науки спереди. Прелесть в том, что авторы статей осознают, что мало написать содержательный текст, но надо сделать его понятным. По этой причине журнал можно рекомендовать всем, у кого душа лежит к естественным наукам.

Узнал я об этом журнале из комментариев к упомянутой выше заметке о цвете неба (спасибо!). Кстати, если не знаете, с каких статей начать осваивать огромный архив, то опять же рекомендую прочитать перечень статей, понравившихся одному из читателей этого блога.

2) Есть более живой и быстрый ресурс, рассчитанный на школьный возраст. «Живая наука» приглашает ставить разные интересные эксперименты, чтобы лучше понять теорию. Плюс в том, что многие опыты очень впечатляют, поэтому сайт может быть полезен учителям и родителям, старающимся привлечь внимание школьников к естественным наукам. Например, можно найти объяснение фокуса с поджиганием собственной руки (естественно, с предупреждением о том, что такие опыты дома делать не стоит). Ну и про объяснение произошедшего авторы не забывают - рядом с описанием эксперимента и видеороликом обязательно идёт поясняющий текст.

3) А где могут лучше понять окружающий мир младшие школьники? Проект «E-mail науки» даёт прямые и краткие ответы на сложные и замысловатые вопросы. Эти статьи могут пригодиться как школьникам, так и их родителям, если собственное чадо их огорошило неожиданной формулировкой. Многие растеряются, услышав вопросы «Почему минус на минус дает плюс?» или «Почему паук не прилипает к своей паутине?», но только не создатели этого сайта. Они уже подготовили большую коллекцию внятных ответов. И ждут новых вопросов :)

Кстати, после изучения детской части этого сайта стоит осмотреть и остальные разделы. Там есть масса интересного! Одна библиотека чего стоит!

Только что я ударился о собственное ограничение - формат этих заметок предполагает три ссылки, а я ещё считаю нужным упомянуть как минимум журналы Квант и Потенциал. Жаль, что это не удалось :)

А какие научно-популярные сайты любите и читаете вы? Какие из них вы бы порекомендовали школьникам?

Почему небо голубое?

Мы наблюдаем это явление каждый день, но задаёмся таким вопросом, как правило, только в детстве. Почему небо голубое? Или почему днём солнце бело-жёлтое, а вечером - красное?

Вроде бы помнится что-то такое из физики, что белый цвет не так прост, как хочется - его можно разложить в сумму всех цветов радуги. Но что из этого следует?

Ещё есть воспоминания о том, что лучи разного цвета имеют различные свойства в разных средах. То есть, конечно, понятно, что в вакууме скорость любых лучей максимальна (равна скорости света). А вот в атмосфере, например, уже можно наблюдать следующее интересное различие:
- синие-фиолетовые лучи движутся медленно, а рассеиваются в среде хорошо (легко преломляются),
- красные лучи движутся быстро, а преломляются плохо.

Другими словами, про изменение цвета солнца стало что-то понятнее: чем ближе наше светило к горизонту, тем больший путь через атмосферу приходится пройти солнечным лучам, чтобы попасть к нам в глаза. Ну а поскольку красные лучи рассеиваются хуже остальных, то именно они определяют для нас цвет солнца. Соответственно, в полдень лучи преодолевают меньшее расстояние по атмосфере, из-за чего меньшее количество не красных лучей успевает разбежаться по другим направлениям. Поэтому днём солнце кажется более белым, чем поздним вечером.

А что же с голубым цветом неба? Там сплошная неясность. Кто-то помнит из научно-популярных книжек или уроков физики о Рэлеевской теории рассеивания. Идея у Джона Рэлея была красивая: если частота света существенно меньше частоты рассеивающего объекта, то рассеяние света происходит без изменения длины волны. Для этого эффекта даже придумали хорошее и понятное название - упругое рассеивание. И долгое время это объяснение считалось правильным и правдивым.

Даже если остановиться прямо сейчас, чтобы, не влезая в дебри непонятной оптики, попытаться пересказать всё это пятилетнему ребёнку, то уже получится очень комично. Недавно мы задавались вопросом, всегда ли надо говорить правду, а вот сейчас видим наглядный пример. Что следует ответить пятилетнему ребёнку на вопрос о причине такого цвета неба, если нельзя (по идейным соображениям) обманывать? Ладно, отвлечёмся на минутку от вопроса «как объяснить?», потому что есть следующий вопрос - «что дальше?»

Целый век назад Леонид Мандельштам осознал, что теория Рэлея слишком красива, чтобы объяснить цвет неба. Дело в том, что теоретические результаты расходились с наблюдениями: рэлеевское рассеивание должно было гаситься интерференцией. Исследователи пришли к мнению, что критически важным моментом является оптическая неоднородность среды.

Короче, мы далеко не все здесь физики, поэтому попытаюсь сформулировать на пальцах: цвет неба определяется типичными размерами неоднородностей, которые возникают в атмосфере. В воздухе постоянно происходит движение молекул, что приводит к образованию областей (на небольшое время) с повышенным и пониженным давлением относительно окружающей среды. И наша атмосфера имеет такие характеристики, что размеры этих неоднородностей такие-то. И именно эти типичные размеры определяют диапазоны волн, которые лучше или хуже будут рассеиваться. Таким нехитрым образом задаётся цвет неба.

Правда ли это? Когда-то считалось правдой, что небо голубое, потому что так покрасили холст, находящийся над нашим материком, подпираемым тремя черепахами. Когда-то считалось, что небо голубое, потому что молекулы воздуха чуть-чуть голубоваты, а толстый пласт атмосферы как раз набирает сильный голубой цвет. Когда-то... Впрочем, надо ли вспоминать старые правды, когда есть новая? Другими словами, мы не очень понимаем, что такое правда и ложь (во всяком случае, нос Буратино не всегда это знает), но иногда запросто берёмся критиковать чужую позицию.

Механизм лжи долгими годами развивался, получив очень сильный толчок в момент зарождения речи. Раньше арсенал обманщика не мог включать в себя, например, подмену смыслов терминов в процессе дискуссии или предоставление чрезвычайно избыточного объёма информации, что практически лишало собеседника возможности не только вычленить важные тонкости, но и понять, о чём идёт речь. Научившись же говорить и писать, люди расширили границы своей лжи, получая индивидуальные преимущества над менее сообразительными сородичами... Увы, забывая, что для популяции это невыгодно. Рекомендую на эту тему статью Алексея Глазкова «Почему мы лжем».

Хорошего вам дня! И пусть вокруг вас будет больше прямых, честных и открытых людей.

О случайных процессах

В комментариях к нашей совместной с Борисом Нечаевым заметке «Что такое случайность?» развернулась очень интересная дискуссия. И сейчас мы предлагаем её продолжить с новыми фактами. Заметка получилась не очень короткой, но, надеемся, познавательной. Ну а перед ответом на вопрос о существовании истинно случайный процессов давайте зададимся другим вопросом: а зачем вообще нужны случайные процессы? Какая нам разница, существуют они или нет?

Если оглянуться по сторонам, то можно найти множество случаев, когда требуется последовательность случайных чисел, предугадать которую никто не может. Простейший пример - выигрышная комбинация лотереи. В книге «Understanding Probability: Chance Rules in Everyday Life» описан следующий случай: в 1920-х годах один из преступных синдикатов Нью-Йорка использовал последние пять чисел ежедневного баланса казначейства США для генерации выигрышной комбинации в своей нелегальной лотерее, поскольку ничего лучше найти не удалось. В то время этого было достаточно для успешной лотереи, но в наши дни, используя современные статистические методы, можно было бы найти регулярность в этих числах, чтобы начать делать ставки на более вероятные исходы.

Схожий пример - онлайн казино, владельцы которых сильно заинтересованы, чтобы их случайные числа никто не мог угадать. Полтора года назад мы уже обсуждали пример того, к чему может привести плохая или неправильная генерация случайных чисел в онлайн покере.

Также случайные числа необходимы для криптографических алгоритмов, используемых для шифрования сетевого трафика в Интернете, банковских транзакций и так далее. Одна из первых уязвимостей, основанная на «плохих» случайных числах была обнаружена в браузере Netscape аж в 1995 году, когда Интернетом пользовалось примерно в сто раз меньше человек, чем сейчас. Другая крупная уязвимость была обнаружена в популярном семействе дистрибутивов линукса Debian совсем недавно - в 2008 году. Разработчики дистрибутива просто закомментировали пару строчек в алгоритме генерации случайных чисел, потому что отладчик из-за этих строк выдавал слишком много предупреждающих сообщений. А когда отладка была окончена, раскомментировать строчки забыли.

Другими словами, случайные числа - вещь крайне важная в самых разных областях человеческой деятельности. Теперь мы рассмотрим способы генерации случайных чисел. И попробуем определить, правда ли они случайны.

В древности и в средние века люди использовали монетки, кубики и другие простые объекты, чтобы генерировать случайные числа. Как мы уже убедились, такой подход плох, поскольку очень трудно сделать объект, который будет выдавать совершенно равновероятные результаты для всех возможных исходов. Этой особенностью предприимчиво воспользовался британский инженер Джозеф Джаггер. В 1873 году он с шестью помощниками отправился в казино и принялся записывать выпадания чисел на рулетках. Обнаружив, что на одном из рулеточных столов некоторые числа выпадают заметно чаще остальных, он принялся ставить деньги на эти числа. После забавной игры в кошки-мышки с владельцами казино, которые заподозрив неладное начали по ночам переставлять столы местами, Джаггер в общей сложности выиграл около 325 тысяч долларов, что в переводе на сегодняшний курс составляет около 5 миллионов.

Кстати, а задумывались ли вы, откуда вообще берётся случайность в таком простом действии, как бросание монетки? Почему, подбрасывая монетку несколько раз, пытаясь сделать это совершенно одинаково, мы всё равно получаем разные результаты? Причиной такого поведения является динамический хаос, присущий многим нелинейным системам. В принципе, в детерминированной системе начальные условия (в нашем примере - положение монетки, сила и направление броска, и так далее) полностью определяют дальнейшую эволюцию, а значит абсолютное повторение начальных условий привело бы к тому же результату. Проблема же в том, что даже небольшое различие в начальных условиях «усиливается», поэтому через некоторое время система ведёт себя совершенно иначе, и монетка может упасть на другую сторону.

Таким образом, для наблюдателя, который не может узнать начальные условия с достаточной точностью, результат будет истинно случайным, в том смысле, что он не имеет возможности его предсказать. Однако не стоит путать случайность и равновероятность: даже истинная случайность (в смысле отсутствия детерминированной модели) не гарантирует того, что все исходы будут выпадать равновероятно - этим и воспользовался вышеупомянутый Джозеф Джаггер.

Сегодня во многих операционных системах и приложениях используются генераторы псевдо-случайных чисел. Такие генераторы также основаны на динамическом хаосе, возникающем вследствие математических преобразований, однако по своей природе являются детерминированными. В этом случае наблюдатель может предсказать результат, угадав начальные условия генератора. Вероятность такого угадывания всегда может быть уменьшена путём увеличения количества возможных начальных состояний (длины ключа), но можно ли это назвать истинной случайностью?

Избавиться от такого угадывания позволяют очень сложные динамические системы, обладающие огромным числом исходных состояний, а также недостаточно точно известными на сегодняшний день физическими законами. В качестве примера можно привести атмосферу нашей планеты, производящую атмосферный шум или проводник со множеством носителей, генерирующий тепловой шум.

Но по-настоящему случайные явления, недетерминированность которых гарантируется законами физики и математическими выкладками, происходят в квантовой механике. Кстати, ученых физиков, до этого считавших, что мы живем в абсолютно детерминированном мире и что все процессы можно однозначно проследить из начальных условий, квантовая механика повергла в настоящий шок. Многие наверное слышали знаменитую фразу Альберта Эйнштейна «Бог не играет в кости», в которой он выразил свое отношение к индетерминизму квантовой механики. Нильс Бор, который кстати любил поспорить с Эйнштейном на тему пристрастия Бога к азартным играм, говорил: «Тот кто не был шокирован квантовой механикой, просто ее не понял».

В чем же коренное отличие квантовых явлений от подкидывания монетки? Оказывается, квантовые объекты подчиняются принципу неопределенности Гейзенберга, который гласит, что мы не можем со сколь угодно большой точностью измерить все необходимые параметры такого объекта. То есть, не можем не просто из-за того, что не хватает технических возможностей, а в принципе не можем. А раз не можем измерить всех параметров, значит не можем и предсказать исход процесса.

Эйнштейна такое состояние дел не устроило, поэтому он предложил мысленный эксперимент, призванный указать на неполноту квантовой механики. Эйнштейн утверждал, что квантовые явления все-таки схожи с подкидыванием монетки, просто все нужные параметры либо еще не открыты, либо скрыты от нас. Эту теорию так и стали называть - теорией скрытых параметров.

Но Эйнштейн в этом случае был неправ, так как Джон Белл математически показал возможность постановки эксперимента, который однозначно опровергнет существование скрытых параметров. С тех пор было поставлено множество таких экспериментов со все большей и большей точностью, и все они подтвердили, что индетерминизм - неотъемлемая черта квантовой механики. Остаётся вопрос о том, являются ли эти эксперименты абсолютным доказательством принципа Гейзенберга или всё же возможна какая-либо альтернативная модель мира... На него может ответить (если ответ существует) только специалист в этой области.

Таким образом, ответ на поставленный нами ранее вопрос утвердительный: да, истинно случайные явления существуют, по крайней мере в рамках существующей модели мира. Но возможно ли их практическое применение? Снова «да»! Исследователи постоянно совершенствуют способы генерации случайных последовательностей при помощи квантовых явлений. К примеру, одна из заметных статей в этом направлении появилась всего чуть более месяца назад в журнале Nature. А вот так выглядит квантовый генератор случайных чисел, который можно подключить к USB или воткнуть в шины PCI и PCI Express.

Хорошего дня!

Потенциал взаимодействия частиц (задача о пружине в кислоте)

Добрый день!

Сегодня мы разберёмся с межмолекулярным взаимодействием и теплом. Зачем нам это? Например, чтобы понять, что происходит при сжатии и растяжении пружины.

Но начнём с простой модельки: представьте себе два воздушных шарика, связанных резинкой. Если мы их будем сближать, то они упрутся друг в друга, а если начнём растаскивать, то натянется резинка, которая их удерживает. То есть, есть некоторый диапазон расстояний между шариками, позволяющий им достаточно свободно перемещаться. Но если их попытаться слишком сблизить или растащить, то можно столкнуться с сопротивлением.

Теперь давайте представим себе две частицы, имеющие нулевой заряд (электрически нейтральные). Пусть они находятся друг от друга очень далеко. Так далеко, что почти не влияют друг на друга. В таком случае разумно говорить, что энергия их взаимодействия равна нулю. Мы ещё можем не понимать, что значит нулевой потенциал взаимодействия, но давайте пока смиримся с этой точкой отсчёта.

А затем мы начнём потихоньку приближать эти две частицы друг к другу. Тут следует вспомнить, что частицы, о которых мы говорим, состоят из положительно заряженного протона и отрицательно заряженных электронов (естественно, суммарный заряд равен нулю). В какой-то момент расстояние между частицами уменьшится до такой степени, что проявится очень интересный эффект - электроны обеих частиц сместятся таким образом, что возникнет сила притяжения (тут правильнее было бы говорить об изменении электронных облаков).

Эту силу притяжения обычно называют силой Ван-дер-Ваальса. В самом деле, если у нас достаточно сближаются электроны одной частицы с протоном другой, то сила их притяжения становится достаточно большой - пренебрегать ею больше нельзя. Эта сила возникает из-за того, что расстояния между разноимёнными зарядами оказывается меньшим, чем между одноимёнными. Так наши частицы начинают всё сильнее притягиваться друг к другу.

И длится это их сближение до тех пор, пока расстояние не станет слишком маленьким. С какого-то момента силу Ван-дер-Ваальса начнёт компенсировать сила отталкивания частиц. Откуда отталкивание? К нему приводит неизбежное на малых расстояниях сближение электронных облаков наших частиц. Одноимённые заряды отталкиваются (а электроны как раз имеют отрицательный заряд). Поэтому чем сильнее нам надо сблизить частицы, тем больше энергии придётся затратить. Это как раз показано на первом рисунке - график стремительно улетает вверх в районе нуля.

Другими словами, есть диапазон «комфортных» расстояний, на которых частицы «готовы находиться самостоятельно», а есть большие и малые расстояния, на которых частицы или почти не замечают друг друга, или мощно пихаются.

Теперь давайте представим пружину - множество частиц, между которыми есть огромное количество прочных связей (из-за этого пружина сама по себе не рассыпается). Когда мы её сжимаем или растягиваем, то совершаем работу, затрачивая энергию. Куда она девается? На смещение части связей из нижней точки потенциальной ямы. Частицам было «комфортно» находиться на тех расстояниях, при которых пружина расслаблена (на самом дне). Но сжимая или растягивая пружину, мы тратим энергию, чтобы заставить их карабкаться на левый или правый склон этого графика. Так энергия запасается в пружине.

И при первой возможности пружина вернётся в исходное состояние - она потратит запасённую энергию на восстановление удобных ей расстояний между частицами.

Теперь уже почти понятно, как можно ответить на недавно заданные вопросы о пружинах:

I. Сжатая пружина, получив возможность вернуться в расслабленное состояние, сделает это. Но так как мы живём не в идеальном мире, то не все связи между частицами сразу смогут вернуться в исходное положение: некоторые частицы останутся «на стенках ямы». То есть, они будут какое-то время «колыхаться» и «пихаться с другими частицами», пытаясь найти наиболее «удобное» для всех положение. А что такое эти колыхания? Это и есть тепло.

II. Если же мы отпускаем пружину в ёмкости с водой, то к описанным выше эффектам добавится ещё и перемещение воды (из-за вязкости): молекулы воды начнут двигаться по всему аквариуму. А что такое перемещение частиц? Это и есть тепло (молекулы воды приобрели скорость, т.е. получили кинетическую энергию). Точнее будет так: движение воды переходит в тепло благодаря трению.

Здесь мы неявно сформулировали, что такое тепловая энергия (её ещё часто называют внутренней энергией). Тепловая энергия - это энергия движения или колебания частиц объекта.

Теперь можно вернуться к исходной задачке о пружине в кислоте. Весь текст выше был нужен для изложения следующей идеи: когда мы растягиваем или сжимаем пружину, то мы нарушаем её устойчивость. Понять это легко: представьте, что мы растянули пружину очень-очень сильно - в какой-то момент она просто порвётся, не выдержав этого. То есть, безгранично запасать энергию в пружине нельзя, так как она сломается.

Из этого напрашивается следующий вывод:
- сжатая пружина находится в менее устойчивом состоянии,
- связи между её частицами не такие мощные, как у расслабленной пружины,
- поэтому кислоте проще их разрушить.

Ну да, это более-менее понятно. Но куда девается потенциальная энергия сжатой пружины при растворении в кислоте? А давайте представим себе проведение этого эксперимента: у нас две одинаковых пружины помещены в кислоту, но одна расслаблена, а вторая сжата. Кислота начинает разрушать связи между частицами пружин, но для разрушения связей сжатой пружины ей требуется меньше энергии.

В реакции растворения можно увидеть две важных компоненты:
- разрушение связей в растворяемом объекте (обычно проходит с поглощением тепла),
- появление гидратов/сольватов(зависит от материала пружины) - это продукты растворения (приводит к выделению тепла).

И если второй процесс для обоих пружин одинаков - мутная жидкость в результате растворения одинаково нагреется, то первый процесс потребует разных затрат энергии (тепла). Результат уже ясен: на разрушение сжатой пружины потребуется меньше энергии, поэтому аквариум, содержавший сжатую пружину, после растворения будет теплее, чем аквариум с расслабленной пружиной.

P.S.
Про каждый из тезисов в этой заметке можно сказать «на самом деле всё не так, а вот так...». Да, я понимаю, что у кристаллов одни свойства, у полимеров другие. Да, реакция растворения - очень сложная штука, имеющая массу нюансов, поэтому про неё так говорить некорректно. Да, все эти фразы о «комфортных расстояниях» - детский сад. Да и с теплотой не всё так просто.

Но я думаю, что если отдавать себе отчёт в том, что мы всегда имеем дело не с реальным миром, а с каким-то его упрощением (моделью), то пользоваться такими соображениями вполне можно (учёные так и делают, только у них модели сложнее).

Ну а за дополнениями, правками, расширениями и пояснениями приглашаю в комментарии.

Энергия пружины и волки

Добрый день.

Сегодня мы начнём разбираться с недавней задачкой о растворении сжатой пружины, а потом перейдём к интересному эксперименту с волками. Итак, в недавней заметке о сохранении энергии мы задались следующим вопросом: куда девается энергия сжатой пружины после растворения пружины в кислоте?

Во-первых, следует обратить внимание вот на какой момент: в исходной заметке была предложена не очень правильная картинка. Дело в том, что центры масс двух пружинок находились на разных высотах. Поэтому потенциальная энергия пружин в поле тяжести была разная: сжатая пружина была ниже. Другими словами, доля потенциальной энергии сжатой пружины была выше (из-за сжатия), а другая доля - ниже (из-за меньшей её высоты). Поэтому мысленный эксперимент не был чистым (здорово, что нашёлся комментатор, заметивший это).

Чтобы исправить эту проблему можно поступить одним из следующих способов:
1) считать, что эксперимент проводится в невесомости (это классическое физическое решение :)
2) растопыривать пружинку в аквариуме чуть выше, чтобы центры масс были на одном уровне (как на исправленной картинке).

Теперь у нас почти всё хорошо с чистотой эксперимента, поэтому можно разбираться с процессом сжатия пружин. Давайте поставим следующие мысленные эксперименты:

I. Возьмём обычную пружину, сожмём её (в этот момент запасём в ней потенциальную энергию), после чего позволим ей распрямиться. Куда делась энергия сжатой пружины? Кстати, чтобы было чище, давайте считать, что этот эксперимент проводится в безвоздушном пространстве.

II. Теперь возьмём ту же сжатую пружинку, но поместим её в ёмкость, например, с водой. И теперь внезапно разожмём пальцы. А куда теперь делась энергия сжатой пружины?

Разобравшись с этими двумя вопросами, мы приблизимся к пониманию задачки о кислоте. Скоро мы разберём нашу задачу III - её понимание будет основано на решениях этих двух. А пока давайте не некоторое время перейдём к удивительному общению с дикой природой. Если сознание сразу хочет поверить в идею Киплинга о маленьком Маугли, воспитанном стаей волков, то представить взаимодействие взрослого человека с опасными хищниками в их естественной среде не очень легко. Но очень интересно!

Ясон Бадридзе несколько лет прожил в стае волков и передал обоим видам важные знания друг о друге. «Людям он рассказал о культуре зверей. Волков научил избегать человека и домашний скот.» - это начало статьи «Между человеком и волком».

Вообще-то у меня сразу возникла ассоциация с фильмом «Аватар», так как в статье интересно описан обмен знаниями. Цитата: «я изначально был экспериментатором, изучал физиологию поведения. Но вскоре осознал, что мы изучаем механизмы того, смысла чего не знаем. Жизнь зверя в природе была почти неизвестна, публикаций о волке тогда почти не было. Я попробовал заняться групповым поведением собак, но скоро понял, что они потеряли многие поведенческие черты. И тогда я решил пожить с волками. Поехал туда же, в Боржомское ущелье, нашел одну семью. Меня интересовало, как формируется поведение, как они обучают волчат охоте…».

И если учёный поселился с волками, чтобы изучать их, то звери приняли его не только из любопытства. Исследователь утверждает, что волки догадались, что их не трогают, пока с ними человек. Цитата: «Взрослые приняли после той встречи, переярки понаблюдали за родителями, поняли, что я не опасен. А потом щенки родились – они вообще не знали, что меня там быть не должно. Дело еще в том, что волки эти меня намного раньше увидели, чем я их. Пока я их следы изучал, они меня физиономически уже знали. И они поняли, что мое присутствие обеспечивает им спокойную жизнь от егерей. Там браконьерство жуткое было: постоянно капканы ставили, гонялись за ними – за волка пятьдесят рублей давали. А я с егерями договорился под угрозой мордобоя: пока я здесь, никаких волков не трогать.»

Эта статья интересным образом перекликается с недавней заметкой о том, что иногда лучше много не думать, а позволить внутренним низкоуровневым процессам взять управление на себя. Цитата:

«А ваше сознание не мешало вам?

Сначала мешало, пока я думал, что делать. А потом – нет, абсолютно. Уже через несколько месяцев. А месяцев через восемь я уже мог точно описать, что делает волк у меня за спиной. Потому что все-таки все время было напряжение: это дикие звери, надо контролировать. И, видимо, это напряжение пробудило третий глаз или как это называется.»

Статья очень интересная, поэтому рекомендую прочитать её целиком. Например, в ней написано не только, что волки не помнят, где спрятали мясо, но и объясняется, почему это хорошо. Или доказывается интересная мысль о том, что охота - это в большой степени традиция, передаваемая из поколения в поколение (цитата: «В одной и той же местности могут жить семьи, которые умеют охотиться только на лося или только на оленя»). Или показан конфликт волчьей неофобии с любопытством - они боятся всего нового, но не могут устоять перед ним. Или продемонстрирован момент непонятного альтруизма - однажды волки спасли учёного от смерти.

Кстати, если вам понравится эта история про волков, то, скорее всего, будет интересно прочитать интересные прогулки с медвежатами (ссылка на них была здесь чуть меньше года назад).

Хороших выходных!

Эксперимент с парой катушек

В предисловии ко своей книге «Краткая история времени от Большого Взрыва до черных дыр» Стивен Хокинг написал, что ему рассказали о том, что каждая включенная в книгу формула уменьшит число читателей в два раза. Тогда он решил вообще обходиться без формул (под конец всё же не удержался - написал знаменитое Е=mc²). Мы пойдём этим же путём - никаких формул. И даже видео про зверушек посмотрим.

Впрочем, дорогие читатели, жизнь показала, что это высказывание было совсем не про вас. Даже если заметку перегрузить формулами, то количество комментариев и просмотров у неё оказывается далеко не нулевым. И это приятно :)

Итак, сегодня мы посмотрим на результаты эксперимента с двумя катушками. В той заметке мы попробовали обсудить теоретический взгляд на задачу. Мнения в комментариях были очень разнонаправленным, поэтому сейчас пора перейти к практике. Установка, которую собрал я, была не очень изящна, но есть удачное видео, наглядно демонстрирующее все существенные моменты (этот ролик прокомментирован на английском языке, но в нём всё понятно и без слов):



Думаю, многие согласятся, что о результатах этого эксперимента можно было заранее легко догадаться. Но для этого было необходимо оглядеть модель целиком, а не привязываться к одному конкретному эффекту. Часто так бывает, что на объект действует несколько сил, поэтому, рассматривая лишь некоторые из них, можно очень сильно ошибиться в прогнозах. В своих расчётах физики всегда игнорируют множество эффектов (в данной задаче, например, никто не будет учитывать притяжение луны). Но они отдают себе отчёт в том, какие воздействия являются ничтожными, а что отбрасывать нельзя.

Полагаю, что после этого видео всё стало понятно. Надеюсь, этот ролик понравится не только вам, но и вашим или знакомым детям. Кстати, сделать такую установку очень легко, а радости и пользы от неё будет гораздо больше, чем от поедания мороженного, например.

Перед тем как пожелать хороших выходных, хочу задать два вопроса:

1. Раздражают ли вас лично вставки роликов в заметки блога? Это первый раз, когда я предлагаю так что-то смотреть, поэтому хотелось бы убедиться, что такая форма никому не мешает. Если почему-то мешает, то буду давать просто ссылку с комментарием.

2. Режет ли вам глаз фраза «Американские учёные разработали новый тип резины, покрышки из которой позволяют автомобилю ехать не только в сорокаградусные горки, но даже и в пятидесятиградусные»? Если да, то что конкретно смущает?

Хорошего вам вечера пятницы и удачных выходных!

Две катушки с нитками

Добрый день!

Сегодня мы продолжим играть с физикой - рассмотрим задачку, при первом взгляде на которую всё станет ясно. Только одни читатели придумают объяснение, ведущее к ответу «вправо», а другие - к ответу «влево». Умом мы понимаем, что механизм не может двигаться одновременно в два направления, но как определить, какую версию отбросить? Нельзя же полагаться на суеверные соображения «первой приходит в голову простая идея, поэтому она не годится». Ведь есть тренированная интуиция, которая запросто может вытолкнуть наверх именно правильный взгляд на процесс.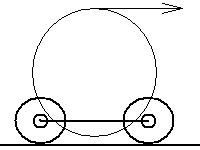

Слева вы видите чертёж: есть две катушки, оси которых надёжно закреплены, есть колесо, к верхней точке которого приложена сила, действующая вправо. Естественно, мы предполагаем, что колесо по катушкам и катушки по полу не проскальзывают.

Теперь рассмотрим две версии происходящего. Первая идея очень проста:

1) Сила приложена вправо, «никто никого не сдерживает», поэтому и вся конструкция поедет вправо. Это объяснение столь короткое и ясное, что даже чертёж не требуется. Но мы уже один раз пробовали рассуждать подобным образом - ничего хорошего из этого не вышло.

Но есть и противоположный взгляд:

2) Приложенная к колесу сила заставляет его вращаться по часовой стрелке. Так как катушки по колесу не проскальзывают, то они начнут поворачиваться против часовой стрелки. А раз так, то катушки поедут по полу влево, увлекая за собой всю систему. Всё выглядит логично, но об такое рассуждение мы уже тоже обжигались.

Как же быть? Какие важные детали мы упускаем? Прежде чем хвататься за карандаш и бумагу, имеет смысл хорошо прочувствовать эту задачку. Можно представить себя колесом, верхнюю точку которого тянут вправо. Потом можно представить себя одной из катушек, вообразив воздействие всех сил (надо смотреть на точки касания колеса и пола). А потом можно поставить эксперимент, если ещё останутся сомнения.

В самом деле, очень легко найти две зубочистки, пару катушек ниток, моток изоленты и две картонки. Кстати, производство самой экспериментальной установки можно поручить детям, предварительно спросив их мнения, куда она поедет - тогда вообще все будут довольны :)

Пожалуйста, присылайте ваши любимые физические задачки в комментарии! Я уверен, что многим будет интересно вспомнить школьные годы или узнать новые стороны пройденных тем.

Хороших вам весенних выходных!

Сохранение энергии

Добрый день!

Многие заметили, что прошлый месяц почти полностью был посвящён математике. Сколько же можно? В самом деле, раз уж первого апреля все желающие отметили день математика, то пора сделать перерыв. Поэтому в предыдущей заметке мы плавно перешли от математики к образованию вообще. А сейчас можем двинуться в любую сторону :)

Например, можно повернуться лицом физике. Наверняка многие со школы помнят о потенциальной энергии:
- поднимая камень вверх, мы запасаем его энергией, а уронив его, высвобождаем накопленную энергию (если уронили на палец, то открывается ещё один мощный источник энергии, судя по громкости восклицаний, но сейчас речь не о нём).
- заводя часы, мы запасаем в пружине потенциальную энергию, которая потом постепенно будет израсходована на перемещение стрелок и «тикание», пока пружина не вернётся в «расслабленное» состояние.

Давайте теперь представим себе два одинаковых аквариума, пару одинаковых пружин и ёмкость с кислотой, способной растворить материал пружин (но не аквариумов). Одну пружину вставим в аквариум вертикально (в «расслабленном» состоянии), а вторую сожмём, чтобы засунуть горизонтально. На сжимание пружины мы потратили энергию - теперь она запасена в пружине. Часть этой энергии можно получить обратно, если доверить пружине совершить работу (сдвинуть какой-то объект, например). То есть, можно считать, что во втором аквариуме с пружиной запасено больше потенциальной энергии, чем в первом.

А теперь заполним оба аквариума кислотой. Через некоторое время мы получим два аквариума с совершенно одинаковыми жидкостями. Возникает резонный вопрос: а куда же делась энергия, которую мы потратили на сжимание второй пружины? Сейчас пружины нет, но энергия же не может исчезнуть «просто так».

Полагаю, скоро в комментариях появятся верные объяснения, поэтому я не советую их сразу читать тем, кто не знал эту задачку. А к остальным у меня следующий вопрос: какие физические задачи у вас ассоциируются с этой? О каких каверзных вопросах вы сразу вспомнили, как только прочитали заметку?

Хорошего дня!

Три задачки

Добрый праздничный день!

Сегодня в нашей рубрике «Три чего-нибудь» будут три задачки: две со ссылками на ответы, а одна - без, но зато все на сообразительность :)

Начнём с простой физической задачки, которую недавно напомнил fdo (осторожно, по ссылке можно случайно прочитать ответ!):

Вступительные экзамены. Стало быть, лето. Жара. На небе ни облачка, солнце светит прямо в окно экзаменационной аудитории. На подоконнике стоит графин с водой. Обычный, граненый. Абитуриент заходит в аудиторию, его просят подойти к окну и потрогать графин. Будущий физик трогает его и ощущает, что сторона, обращенная внутрь аудитории, теплее, чем обращенная к окну. Экзаменаторы просят объяснить наблюдаемое явление. Собственно, в этом и состоит вопрос.

Эту историю часто пересказывают выпускники ВУЗов разных городов, уверенно называя имена экзаменаторов, номера аудиторий и прочие уточняющие моменты. Короче, каждый старается приобщиться к старинной легенде. Но от этого она не становится менее забавной :)

Следующая задача совсем не про физику. Её предложил alexsmail:
Если известно, что
   2 + 3 = 10
   7 + 2 = 63
   6 + 5 = 66
   8 + 4 = 96,
тогда
   9 + 7 = ?

По ссылке выше предложен способ проверить правильность своего ответа (ввести свою версию в форму). Эта задачка тоже очень простая, но следующая является настоящей логической проблемой.

Итак, опять fdo поделился интересной формулировкой (и опять будьте осторожны с этой ссылкой, чтобы случайно не прочитать ответ):

На некотором острове местные жители делятся на правдолюбов и лжецов. Они вежливые люди и всегда отвечают на вопросы чужеземцев, ну, естественно, если могут ответить. Но при этом правдолюбы всегда отвечают правду, а лжецы всегда лгут. И вот представьте себе: Вы попадаете на этот остров. Вы встречаете аборигена. Как, задав ему один вопрос, требующий ответа «Да» или «Нет», выяснить, сколько у него детей?

Прелесть задачки в том, что сначала кажется, что невозможно получить так много информации, задав всего один вопрос. У меня несколько дней ушло на эту задачу, но оно того стоит!

Как обычно, прошу для статистики поделиться в комментариях своим видением этих задач. Примерный вид пусть будет, например, таким:

1. Нам такое ещё в детском саду рассказывали,
2. Решил быстрее, чем читал условие,
3. Пока думаю :)

Хорошего дня!

Катушка с нитками

Вчера мы начали обсуждение одной старинной и яркой физической задачки, позволяющей внимательнее посмотреть со стороны на то, что же нам подсказывает интуиция. В комментариях к той заметке можно найти очень ясные и подробные выкладки, показывающие, почему и в предложенном случае тело будет двигаться туда же, куда его тянут (хоть и кажется, что должно двигаться в противоположную сторону, хотя только что казалось, что должно двигаться в ту же).

Очень ценно то, что многие заметили подвох, не поверив в красивые слова. Но доказывает ли это, что объект всегда будет идти туда, куда его тянут? Давайте рассмотрим ещё один пример (опять с синими нитками :)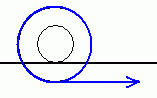

Пусть наша катушка устроена следующим образом: узкая ось, на которую щедро и аккуратно намотали много витков ниток, лежащая на двух рельсах (линейках, например). Мы тянем эту катушку вправо за нитку, а она начинает двигаться влево.

Логика прежняя: тянем нитку, поэтому возникает вращение катушки против часовой стрелки, из-за чего она, естественно, укатывается влево. Для этого опыта достаточно взять одну катушку и две линейки или два карандаша (или ещё два чего-нибудь одинакового и не слишком скользкого, чтобы силы трения хватало).

Здесь важно прочувствовать разницу с предыдущим примером. Понятно, что отношение радиусов у катушки поменялось, но надо ясно видеть, почему из-за этого так сильно развернуло всю конструкцию. Если есть вопросы, то приглашаю в комментарии - как показала вчерашняя дискуссия, очень многие прекрасно понимают, какие силы возникают. И, что тоже очень важно, активные специалисты умеют понятно и подробно всё пояснить, поэтому разберутся все желающие.

Надеюсь, мы закроем все вопросы об этой задачке до Нового года, потому что после него мы приступим к чуть более хитрой конструкции. Ну а если вы уже всё поняли, то приглашаю прочитать о головоломке, для решения которой надо не просто посетить в школе несколько уроков физики, но и достаточно глубоко проникнуться некоторыми темами. Надеюсь, вам понравится!

Хорошего дня и весёлой подготовки к празднованиям!

На плоской поверхности

Интуиция помогает нам постоянно, так как обеспечивает принятие быстрых решений, не очень напрягая. Если бы мы думали над каждой мелочью, то почти ничего не успевали бы в своей жизни. Но у нас есть этот замечательный инструмент. И его периодически надо калибровать.

Что вы ответите, если сейчас неожиданно прочитаете следующий вопрос: «Куда двинется объект, стоящий на горизонтальной поверхности, если его потянуть вправо?»

Интуиция сразу подсказывает, что тело тоже должно двинуться вправо, так ведь? Но если мы тянем вправо железнодорожный локомотив за рычаг, который отвечает за запуск двигателя? Тогда всё зависит от остальных рычагов: поезд запросто может поехать влево.

Хорошо, давайте договоримся, что наш объект не имеет никакой электроники, кнопки не могут запустить двигатель, потому что на борту нет ни нефтепродуктов, ни угля, ни газовых баллонов. Что тогда?

Тогда, наверное, потянув вправо, мы получим и движение вправо, верно?

Но если у нас есть конструкция из механических часов, которым вместо стрелок приделали колёса, а тянем мы за верёвочку, привязанную к клину, заблокировавшему механизм? В таком случае, потянув вправо, мы запустим часы, из-за чего они преспокойно уедут влево.

Ладно, никто не спорит с тем, что эту задачу нельзя назвать полностью определённой. Но давайте подумаем, а что будет, если наш объект не имеет никакой накопленной энергии? Тогда вариант с часами не пройдёт, так как их энергия запасена в пружине.

Пока вы думаете, я напомню старую статью о правдоподобных аргументах - в ней мы разбирали менее физические, но более актуальные для многих ситуации. Тонкость в том, что зачастую мы можем считать правильными два аргумента, доказывающие совершенно противоположные позиции. Работа в режиме «если звучит правдоподобно, то считать это верным, чтобы не терять время» - это особенность нашей интуиции, которая иногда проявляется совсем не вовремя. И именно по этой причине я стараюсь обращать внимание на задачки, выявляющие сбои нашего внутреннего предсказателя.

Если мы прикладываем к объекту силу вправо, а внутри его нет никакой запасённой энергии, то он должен начать двигаться вправо. Это же очевидно! Точно?

Давайте рассмотрим обычную деревянную катушку с синими нитками (как на рисунке справа). Если её аккуратно тянуть за нитку вправо, то катушка начнёт двигаться влево, верно? Мы же заставляем крутиться катушку против часовой стрелки, поэтому она направится в сторону, противоположную силе, приложенной к нити. Не верится? Эксперимент легко поставить у себя дома!

Я уверен, что многие видели этот пример в книгах Перельмана или других удачных сборниках для школьников. Наверняка кто-то придумывал подобные конструкции сам. И теперь, видя этот пример своими глазами, мы отчётливо понимаем, что на исходный вопрос хотелось ответить «вправо», но это был напрасный позыв (в общем случае). Впрочем, в большинстве ситуаций интуиция отлично справляется. Так ведь? ;)

Кстати, а все ли понимают физическую суть предложенного процесса с катушкой ниток? Если мы прикладываем силу вправо, то почему катушка едет влево? Какая сила её двигает? Понимание этого момента пригодится нам в одной из следующих заметок о чуть более сложной конструкции, поэтому предлагаю обсудить это сейчас в комментариях.

Хорошего дня!

Что думать? Трясти надо!

Одна смышлёная обезьяна увидела, как другая
усиленно трясет дерево с бананами, а они не падают.
Тогда первая пытается подсказать: "Слушай,
может, надо подумать? может палку взять в руки?".
А та ей отвечает: «Что тут думать, трясти надо!».

В заметке про хорошие подарки я обещал рассказать о головоломке, которую сделал мне добрый друг. Она имеет прямое отношение к эпиграфу, показывая типичный подход к решению :)

Игрушка состоит из двух одинаковых деревянных деталей. Конечно, изначально виден только собранный крест (и с ним вообще ничего не понятно), но когда "фокусник" за считаные мгновения разбирает его у себя за спиной, то получаем в руки две идентичные детальки. На второй картинке справа Вы можете видеть примерную схему такой детали. В нижней части есть сквозное отверстие, а в верхней - два штыря, которые свободно ходят (на рисунке - влево-вправо), но не выпадают наружу, так как закреплены внутри деревянного корпуса.

В собранном состоянии получается надёжно скреплённый крест, ведь штыри одной детали входят в отверстия второй (и наоборот). И как бы мы ни поворачивали головоломку, если сила тяжести выводит одни штыри из отверстия, то противоположный штырь тут же опускается внутрь.

Предложивший головоломку ждёт минут 15-30, наблюдая за разными махинациями (лишь бы физическую силу особо не прикладывали)... А потом намекает, что открыванию такого креста была посвящена целая длинная тема на уроках физики примерно в 8 классе. Одних это озадачивает, других - раззадоривает. После этого трясти игрушку начинают ещё активнее. В это время и вспоминается какая-нибудь вариация анекдота из эпиграфа.

А теперь, как обычно - опрос. Напишите, пожалуйста, в комментарий один из следующих статусов:
1) игрушку такую давно знаю, в своё время быстро справился,
2) игрушку такую давно знаю, в своё время справился, но пришлось повозиться,
3) первый раз вижу, но понял уже, о какой теме на уроках физики речь,
4) первый раз вижу, ещё не понял принципа открывания,
5) не понял, как устроена головоломка (чертёж и описание не подробны).

Скоро будет разбор этой головоломки. Кстати, она является хорошим подарком ещё и по той причине, что её можно сделать своими руками :)