С Новым годом!

За прошедший год я выпил чуть меньше полутора литров вина, примерно 150 миллилитров коньяка и около 100 миллилитров водки. Кому-то нравится больше, а мне хватает столько. Благо, друзья и родственники понимают, что я не люблю пиво, не особо радуюсь опьянению и так далее, поэтому почти никогда не настаивают.

Увы, в некоторых компаниях иногда приходится выслушивать странные упрёки «ты что - не русский?» или «совсем не мужик?» (как будто именно пьянство является необходимым признаком русского мужчины) Интересно, что даже женщины, страдающие от того, что их мужья «не просыхают», продолжают следовать сложившемуся десятилетия назад шаблону - уговаривают выпить каждого при любой возможности. Трудно это понять... Поэтому я старюсь избегать подобных встреч.

Нет, у меня не было проблем с «больной головой на утро», здоровья вполне хватает, чтобы выпить «сколько надо». По молодости всякие глупости бывали... Но сейчас уже нет к этому интереса.

Поэтому я за питьё в меру. Пока человеку мероприятие нравится, пока он не теряет над собой контроля, пусть отдыхает. Алкоголь - не самая страшная беда, не самый бесполезный продукт. Я думаю, есть много случаев, когда с алкоголем получается лучше, чем могло бы быть без него. Но нужно понимать, где следует опасаться неожиданных серьёзных проблем из-за выпивки.

Поэтому желаю вам отметить наступление очередного года,
- если возможно, то увидевшись с родителями, бабушками и дедушками (им всегда будет мало вашего тепла, поэтому угостите их капелькой счастья - обнимите крепче),
- хорошо пообщавшись со всеми родственниками (очень приятно знать всю свою большую семью - это придаёт сил и наполняет жизнь новым смыслом),
- встретившись или связавшись со всеми друзьями.

Я мечтаю чаще общаться с близкими людьми, но обычно есть масса приоритетных дел, постоянно откладывающих самые приятные моменты. Именно поэтому я поздравляю вас не столько с каким-то очередным %названием праздника%, сколько с возможностью зарядиться позитивным человеческим общением, стать ближе родным людям и роднее близким.

Не надо ничего выдумывать в последний день! Если есть хороший подарок, то он не обязан ждать праздника, а если его нет, то глупо покупать ерунду в магазине. Гораздо лучше сделать своими руками торт, чтобы потом его всем вместе съесть! :)

Хорошего вам празднования!
Пусть будет тепло и светло, весело и вкусно, радостно и приятно!

До встречи в 2010 году!

Катушка с нитками

Вчера мы начали обсуждение одной старинной и яркой физической задачки, позволяющей внимательнее посмотреть со стороны на то, что же нам подсказывает интуиция. В комментариях к той заметке можно найти очень ясные и подробные выкладки, показывающие, почему и в предложенном случае тело будет двигаться туда же, куда его тянут (хоть и кажется, что должно двигаться в противоположную сторону, хотя только что казалось, что должно двигаться в ту же).

Очень ценно то, что многие заметили подвох, не поверив в красивые слова. Но доказывает ли это, что объект всегда будет идти туда, куда его тянут? Давайте рассмотрим ещё один пример (опять с синими нитками :)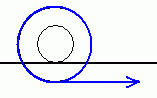

Пусть наша катушка устроена следующим образом: узкая ось, на которую щедро и аккуратно намотали много витков ниток, лежащая на двух рельсах (линейках, например). Мы тянем эту катушку вправо за нитку, а она начинает двигаться влево.

Логика прежняя: тянем нитку, поэтому возникает вращение катушки против часовой стрелки, из-за чего она, естественно, укатывается влево. Для этого опыта достаточно взять одну катушку и две линейки или два карандаша (или ещё два чего-нибудь одинакового и не слишком скользкого, чтобы силы трения хватало).

Здесь важно прочувствовать разницу с предыдущим примером. Понятно, что отношение радиусов у катушки поменялось, но надо ясно видеть, почему из-за этого так сильно развернуло всю конструкцию. Если есть вопросы, то приглашаю в комментарии - как показала вчерашняя дискуссия, очень многие прекрасно понимают, какие силы возникают. И, что тоже очень важно, активные специалисты умеют понятно и подробно всё пояснить, поэтому разберутся все желающие.

Надеюсь, мы закроем все вопросы об этой задачке до Нового года, потому что после него мы приступим к чуть более хитрой конструкции. Ну а если вы уже всё поняли, то приглашаю прочитать о головоломке, для решения которой надо не просто посетить в школе несколько уроков физики, но и достаточно глубоко проникнуться некоторыми темами. Надеюсь, вам понравится!

Хорошего дня и весёлой подготовки к празднованиям!

На плоской поверхности

Интуиция помогает нам постоянно, так как обеспечивает принятие быстрых решений, не очень напрягая. Если бы мы думали над каждой мелочью, то почти ничего не успевали бы в своей жизни. Но у нас есть этот замечательный инструмент. И его периодически надо калибровать.

Что вы ответите, если сейчас неожиданно прочитаете следующий вопрос: «Куда двинется объект, стоящий на горизонтальной поверхности, если его потянуть вправо?»

Интуиция сразу подсказывает, что тело тоже должно двинуться вправо, так ведь? Но если мы тянем вправо железнодорожный локомотив за рычаг, который отвечает за запуск двигателя? Тогда всё зависит от остальных рычагов: поезд запросто может поехать влево.

Хорошо, давайте договоримся, что наш объект не имеет никакой электроники, кнопки не могут запустить двигатель, потому что на борту нет ни нефтепродуктов, ни угля, ни газовых баллонов. Что тогда?

Тогда, наверное, потянув вправо, мы получим и движение вправо, верно?

Но если у нас есть конструкция из механических часов, которым вместо стрелок приделали колёса, а тянем мы за верёвочку, привязанную к клину, заблокировавшему механизм? В таком случае, потянув вправо, мы запустим часы, из-за чего они преспокойно уедут влево.

Ладно, никто не спорит с тем, что эту задачу нельзя назвать полностью определённой. Но давайте подумаем, а что будет, если наш объект не имеет никакой накопленной энергии? Тогда вариант с часами не пройдёт, так как их энергия запасена в пружине.

Пока вы думаете, я напомню старую статью о правдоподобных аргументах - в ней мы разбирали менее физические, но более актуальные для многих ситуации. Тонкость в том, что зачастую мы можем считать правильными два аргумента, доказывающие совершенно противоположные позиции. Работа в режиме «если звучит правдоподобно, то считать это верным, чтобы не терять время» - это особенность нашей интуиции, которая иногда проявляется совсем не вовремя. И именно по этой причине я стараюсь обращать внимание на задачки, выявляющие сбои нашего внутреннего предсказателя.

Если мы прикладываем к объекту силу вправо, а внутри его нет никакой запасённой энергии, то он должен начать двигаться вправо. Это же очевидно! Точно?

Давайте рассмотрим обычную деревянную катушку с синими нитками (как на рисунке справа). Если её аккуратно тянуть за нитку вправо, то катушка начнёт двигаться влево, верно? Мы же заставляем крутиться катушку против часовой стрелки, поэтому она направится в сторону, противоположную силе, приложенной к нити. Не верится? Эксперимент легко поставить у себя дома!

Я уверен, что многие видели этот пример в книгах Перельмана или других удачных сборниках для школьников. Наверняка кто-то придумывал подобные конструкции сам. И теперь, видя этот пример своими глазами, мы отчётливо понимаем, что на исходный вопрос хотелось ответить «вправо», но это был напрасный позыв (в общем случае). Впрочем, в большинстве ситуаций интуиция отлично справляется. Так ведь? ;)

Кстати, а все ли понимают физическую суть предложенного процесса с катушкой ниток? Если мы прикладываем силу вправо, то почему катушка едет влево? Какая сила её двигает? Понимание этого момента пригодится нам в одной из следующих заметок о чуть более сложной конструкции, поэтому предлагаю обсудить это сейчас в комментариях.

Хорошего дня!

Терминал D аэропорта Шереметьево

Добрый день. Сегодня я собирался предложить добрую физическую задачку, но коварная судьба распорядилась иначе - опять будет дневниковая запись. А задачку мы разберём в следующий раз :)

Особенность человеческого восприятия состоит в том, что при хорошем внутреннем настрое мы реже концентрируемся на минусах ситуации, активно радуясь положительным моментам. А в плохом настроении «всю правду» видим. Я уверен, что разработчики Шереметьево-3 (терминала Д) многое продумали, что они старались. Но это сложно оценить, если видна масса недостатков.

Итак, как добраться в новый терминал D из Шереметьево-2? Есть специальный автобус, который должен ходить по расписанию каждые 15 минут. Он не придерживается расписания, поэтому я и ещё большая толпа ждали вместо 15 запланированных минут все 30. Впрочем, это ничего не испортило (по причинам, о которых будет рассказано ниже), а только слегка усугубило картину.

Приехав в Шереметьево-3, мы дружно направились по указателям «Регистрация/Check In», пока не упёрлись в пару лифтов и табличку «едьте на 3 этаж». За несколько следующих часов я так и не смог найти открытых лестниц (вероятно, они спрятаны за закрытыми дверями). Это как минимум опасно, так как нет ясности, куда бежать при задымлении, например. Ну а для опаздывающих это ещё и очень неудобно, так как им приходилось просить остальных людей позволить уехать на лифте без очереди.

С лифтами там вообще всё очень идиотично: есть нормальные (которые хорошо спрятаны, но мне их удалось найти), а есть распространённые - эти умеют ездить только на 2 и 3 этаж (с любого). Это приводило к тому, что люди, желающие спуститься на первый уровень, вызывали такой лифт, не зная подвоха. И после этого они начинали терять своё и чужое время, пытаясь заставить его спуститься. Проблема в том, что неспособность лифта ехать на первый этаж неочевидна: кнопки 1 и 2 отправляли лифт на второй этаж, а кнопка 3 - на третий. Из-за этого лифты были постоянно заняты запутавшимися людьми, что создавало большую очередь из желающих подняться на регистрацию с первого этажа.

Дальше - хуже. Безумные очереди на регистрацию и отсутствие приоритета для тех, кто «вот-вот опоздает». Сколько раз в своей жизни я видел огромные толпы на регистрации, столько же раз видел и желание аэропорта не усугубить ситуацию. В нормальных терминалах громко объявляли «пассажиры, стоящие на регистрацию на такой-то рейс, срочно выходите из той очереди, где сейчас пытаетесь стоять, так как вас быстро обслужат на стойке номер такой-то». И это позволяет оперативно убрать из зала несколько десятков человек, которые ещё имеют возможность улететь по своим билетам. В Шереметьево-3 сделано наоборот: стойки регистрации закрывались на наших глазах. Люди, которые почти достояли до получения заветного посадочного талона, получали грубое «идите отсюда в другую очередь, я закрываюсь». Работающих стоек мрачно не хватало, поэтому всё больше и больше людей переходило из длинных очередей на регистрацию в безумно длинную очередь на обмен билетов. Сотрудников не хватало и там (из четырёх окошек работало только два).

Была ещё одна суровая очередь - на получение места в гостинице. Ирония состояла в том, что сотрудница, которая должна была её обслуживать, куда-то выходила на полтора часа. Когда разъярённые матери с детьми смогли добыть представителя авиакомпании, он очень удивился пустому окошку. И сказал, что попытается найти соответствующую сотрудницу. И где-то минут через 30 нашёл её. Но это не помогло: вроде бы сначала были какие-то проблемы с компьютером, а потом вскрылось отсутствие мест в гостинице... Благо, мне это не было нужно, поэтому дальнейшей судьбы тех людей я не знаю. Я видел только, что многие люди, отчаявшись попасть в гостиницу, засыпали на своих куртках прямо на полу, выбрав не очень людное место. Почему на полу? Потому что кресел очень мало! Сесть невозможно, а стоять в духоте так долго тоже не получается.

В новостях можно прочитать, что в терминале D были проблемы с системой сортировки багажа. И это чистая правда: многие люди в очередях рассказали, что они не успели попасть на свои стыковочные рейсы, потому что им несколько часов не могли отдать багаж с предыдущего рейса. Но дело не только в этом. Масса людей могла бы давно уже улететь, если бы хватало работников на стойках регистрации. Но их не обслуживали, из-за чего росли очереди на замену билетов, на получение номера в гостинице, на получение талонов на питание и так далее. В тесном и душном зале не было возможности приобрести воду, поэтому люди тоже добрее не становились (вода продавалась на первом этаже, но добраться туда крайне трудно, так как лифт не опускается так низко, а лестниц нет).

Все эти очереди могли быть гораздо короче, если бы хватало квалифицированных сотрудников. На вопрос о том, почему мы видим так мало работников в столь критический момент, сотрудники по секрету рассказали, что недавно было большое сокращение, поэтому работать некому... А вокруг опоздавших на свой самолёт людей издевательски мигали рекламные щиты с пожеланием приятного полёта.

Ну и всякая мелкая критика, конечно, есть:
- Очень тесный зал ожидания: здоровенные колонные вентиляции постоянно стоят на пути, практически невозможно пройти, не задев при этом других людей.
- У многих рейсов неожиданно менялся номер выхода (иногда несколько раз), поэтому сотни людей стремительно проносились по этой тесноте, снося всё на своём пути.
- Нигде не висят часы, хотя всем постоянно нужно знать время. В нормальных аэропортах на каждом табло тикает время, здесь же надо каждый раз доставать мобильник, а потом вычислять местное время.
- В зале ожидания очень маленькие и немногочисленные табло с информацией о вылетающих самолётах. Опять же, в нормальных аэропортах нет проблемы так расположиться, чтобы видеть данные своего рейса. Здесь же надо пробежать большое расстояние, чтобы упереться в толпу таких же вглядывающихся в крошечные буковки маленького экранчика. А информация эта необходима перед посадкой, так как номера выходов часто «обновлялись», а время вылета изменялось.

Теперь о хорошем:

1. Хоть многие пассажиры не могли сдержаться, срываясь на бедных сотрудниках аэровокзала, очень многие люди вели себя более чем достойно: поддерживали друг друга, старались вести весёлый и непринуждённый разговор, успокаивая самых нервных. Много добрых дел было сделано до того, как нуждающийся успевал даже попросить о чём-то: люди дарили матерям с детьми бутылочки воды, помогали иностранцам сориентироваться в ситуации, переводили их вопросы сотрудникам аэропорта и так далее. В такие сложные моменты отчётливо видно, как у нас много позитивных и благородных людей. Отдельно хочу сказать спасибо рядовым сотрудникам аэропорта, которые находили в себе силы стараться оперативно решать проблемы пассажиров в очень нервной обстановке.

2. В новом терминале чистые, просторные и удобные туалеты. Впрочем, люди в аэропорт не за этим приезжают.

3. Всё было тяжело, медленно и неопределённо, но работало. Люди получали новые билеты на более поздние рейсы, пассажирам с детьми старались давать места в бизнес-классе, пытаясь как-то облегчить жизнь. Я не могу точно сказать, очереди скорее росли или укорачивались, так как провёл в этом дивном месте всего около 5 часов. Но движение шло, поэтому напряжение от неопределённости на лицах многих людей постепенно сменялось более-менее спокойной усталостью.

Поэтому мораль сейчас такая: ближайшие месяцы лучше не летать через этот терминал, пока там порядок не наведут. Проблемы там разрешимые, но я не верю, что с ними быстро справятся (терминал уже более месяца открыт, но до сих пор так странно работает). Ну а если других вариантов нет, то берите билеты так, чтобы оставалось хотя бы 6-7 часов между рейсами.

Удачи!

Центрифуга и пять пробирок

Добрый день, дорогие читатели!

Приношу извинения перед всеми, кто всерьёз начал беспокоиться, заметив долгое отсутствие новых заметок. У меня всё отлично! Сейчас я в романтической поездке, посвящённой юбилею свадьбы. Хоть интернет по дороге и попадался, но найти время даже для чтения комментариев было нелегко: масса новых впечатлений перегружает голову, интересные люди и курьёзные моменты завораживают, от обилия достойных внимания вещей кружится голова. Надеюсь на понимание :)

Впрочем, сейчас я начинаю потихоньку «возвращаться в реальность», поэтому в ближайшее время все получат ответы на письма и комментарии. У нас ещё есть полторы недели в этом году - их надо провести с толком!

Хоть данная заметка и начата в жанре «лытдыбр», сейчас мы плавно перейдём к математической задачке, которую недавно решила моя любимая женщина - биолог по специальности. Рассмотрение этой задачки, например, позволяет дать ответ на весьма распространённый вопрос: «А зачем биологу надо знать математику?»

Итак, представьте себе лабораторную центрифугу на 12 пробирок. Их обычно используют для осаждения, разделения фаз и так далее. Но нам это сейчас неинтересно, а важно понять, как она устроена. Наша центрифуга - это вращающаяся ось, на которой закреплён диск с двенадцатью равномерно распределёнными по окружности отверстиями. Для запуска установки необходимо обеспечить её уравновешенность. Другими словами, центр масс должен оказаться на оси (иначе центрифуга будет прыгать по столу, как советская стиральная машинка при сушке белья, что приводит к поломкам).

Разместить две одинаковые пробирки легко - достаточно воткнуть их в противоположные отверстия. Аналогично можно поместить любое чётное число пробирок. Но как быть, если у нас есть пять одинаковых пробирок?

Пожалуйста, напишите в комментариях не только свой ответ, но и путь, которым его получили - это всегда интересно.

Хорошего дня!

Заявление: прошу вернуть украденное

Последнее время коммунальные службы повадились часто менять свои названия и номера счетов, на которые следует производить оплату (хорошо, что остаются в тех же помещениях, поэтому искать их не приходится после этого). Такие изменения приводят к тому, что вносимые в систему платежи попадают на счета «прежней» организации, хотя обслуживает уже «новая». И эта новая служба вдруг замечает, что люди ей должны, поэтому начинает потихоньку начислять пеню.

Короче, именно благодаря этой пене я недавно заметил, что произошло достаточно большое недополучение средств, отправленных на оплату электричества. На конец одного месяца у меня было оплачено X киловатт-часов, а на начало следующего вдруг стало X-6000... Из-за этого возник большой долг, начала капать пеня... Хорошо хоть заметил вовремя. Увы, времени было мало, поэтому я просто в срочном порядке погасил этот долг. А через некоторое время пришёл разбираться, как же так вышло.

Завершение истории - я написал сегодня в прежнюю коммунальную службу типовое заявление (у них образец этого дела на стене висел) со следующим смыслом: «Прошу перевести деньги, оставшиеся у вас на моём счету, в организацию, которой передана функция приёма моих средств за коммунальные услуги». Или как-то так. Соответственно, на словах они мне пообещали через месяц произвести перевод денег, поэтому всё скоро выровняется. До следующей смены названия и номеров счетов.

Суть истории - они мне сами назвали сумму, которую задержали у себя, не глядя в принесённые мною квитанции об оплате. Другими словами, «старая организация» прекрасно знает, кому и сколько должна. Но не спешит переводить эти деньги, пока человек не придёт ногами (а ведь очень легко сделать автоматическую пересылку оставшихся средств «новой организации»). А что же она тогда делает с теми деньгами, за которыми никто не приходит? Я вот совершенно случайно заметил, что возник такой казус. И трудно оценить, сколько раз до этого я таких хитростей не замечал.

Мораль: при оплате коммунальных услуг необходимо проверять непрерывность значений, чтобы случайно два раза за одну услугу не заплатить (как это сделал я, увидев большой долг). Платить на большие сроки впрок - хорошая затея. Но если так делать, то можно получить неожиданную проблему в виде потерявшихся не на тех счетах денег. И тогда придётся или забыть о них, или приходить во второй четверг месяца с 10 до 11 часов, чтобы подать заявление. Мелочи жизни, конечно, если это как раз попутно. А если много других дел, то раздражает.

Удачи вам и хорошего окончания недели :)

И так можно

Совершенно понятная и очень правильная мысль иногда мешает. Например, некоторые ученики часто пытаются одолеть задачу не новым подходом (которому посвящён урок), а своими старыми умениями. При этом каждый из них говорит: «Не хочу вникать в новую тему, потому что я и так эту задачу смогу решить». В самом деле, если ответ правильный, то какая разница, как именно решать?

Но разница есть: ученики, освоившие новый метод, справляются с каждой задачкой за 3-5 минут, постепенно переходя от простых упражнений к тяжёлым. А наш упорный любитель старых методов на каждую из простых задач тратит по 20-30 минут и несколько тетрадных листов. Поэтому до средних и сложных упражнений он вообще не добирается. И из-за этого он даже не понимает, что его желание доказать ненужность нового подхода не позволяет ему увидеть те сложности, которые невозможно одолеть старыми методами.

Кто-то скажет, что надо сразу давать такие задачи, чтобы их невозможно было решить старыми методами. Но проблема в том, что очень часто такие задачи не могут быть наглядным примером. Всё же учиться надо на чём-то простом, чтобы ученик мог увидеть задачу целиком. А сложная проблема не годится для обучения новой теме. Впрочем, иногда удаётся найти простую и оригинальную задачку, что даже ненавистники новых тем смиряются - без нового знания её не решить.

В жизни тоже часто надо рассматривать несколько подходов к задаче, чтобы выбрать самый короткий и простой. Если идти длинным и сложным путём, то можно насобирать высокую вероятность ошибки в каких-то простых рутинных операциях. Если действий много, то ошибиться легко, но трудно найти этап, на котором произошла ошибка, чтобы её исправить.

Приведу классическую задачку, на примере которой данный эффект хорошо виден:

Кубок по футболу разыгрывается по олимпийской системе; ничьих не бывает, к следующему туру допускается только победившая команда, проигравшая же выбывает из розыгрыша. Для завоевания кубка команда должна только побеждать (нельзя проигрывать). На участие в розыгрыше кубка поданы заявки от 16389 команд. Сколько матчей будет сыграно, пока определится обладатель кубка? (Не путать число матчей с числом туров!)

Мы тут часто решаем забавные математические задачки с подвохом, но сегодня не тот случай. Это простая постановка, в которой никто никого не собирается обманывать :)

Я предлагаю сделать сейчас небольшую паузу и найти свой собственный ответ на эту задачу.






Итак, поздравляю с успешным решением задачи. Да, она простая, но всеми силами приглашает решить себя сложным путём.

Сначала расскажу сложный путь:
- в финале играют две команды - это один матч,
- в двух полуфиналах играют две пары команд - это два матча,
- в четырёх четвертьфиналах играет четыре пары команд - это ещё четыре матча,

И так далее. Честно выписываем эти степени двойки, пока не доходим до строчки
- в 8192-ти 8192-финалах играет 16384 команд - это ещё 8192 матча.

Что делать дальше? У нас участвует 16389 команд, а мы придумали как устроить игру для 16384 команд. Куда деть ещё пять? Можно выбрать для них случайно пятерых соперников, чтобы они за дополнительные пять игр установили, кто из них лучше.

Выходит, наш ответ такой: 1+2+4+8+16+32+...+8192+5.

Это Длинно? Да, длинно! Скучно? Конечно, очень скучно!

Тем, кто решил задачку подобным образом, я предлагаю прерваться на несколько минут, потому что есть очень простое и короткое рассуждение. Оно не позволяет наделать ошибок в таком большом суммировании, не требует воображения, чтобы определиться с тем, куда деть «лишние пять команд»... Оно короткое и изящное.






Если вы это читаете, значит уже нашли быстрое решение, а сейчас хотите узнать, бывает ли ещё быстрее. Или пока не нашли, но узнать уже хочется - тоже понятное желание. Итак, в результате каждого матча одна из команд выбывает, а нам надо определить, сколько пройдёт матчей до того, как останется всего одна команда. Раз команд изначально 16389, значит надо, чтобы выбыли 16388 из них, чтобы осталась ровно одна. Это значит, что требуется 16388 матчей. Всё! :)

Данная задачка была опубликована, например, в книге «Смотри в корень!» Петра Маковецкого. Саму книгу я уверенно рекомендую для чтения школьникам и их родителям, так как в ней приводятся интересные постановки проблем, совместное обсуждение которых открывает глаза на интересные моменты в устройстве нашего мира. Увы, её давно не переиздавали, поэтому остаётся только читать в интернете (или на электронной читалке).

Напишите в комментариях, пожалуйста, какие вы знаете задачки с аналогичным свойством: есть очень простое решение, но длинное бросается в глаза раньше.

Хорошей недели!

Вирт и Гришковец

В сегодняшний день информатики мы вспомним Никлауса Вирта и продолжим осмотр выражений, имеющих несколько значений. Нынешняя тема - для кого-то обидное, а для кого-то желанное звание «обычный человек».

Что общего между Никлаусом Виртом и Евгением Гришковцом?
Ну, кроме букв «в», «и» и «р» в фамилиях :)
И того, что они оба родились в середине февраля.

Один создал Паскаль, Модулу-2 и Оберон, является, например, лауреатом Премии Тьюринга. А другой создал «Как я съел собаку», «Одновременно» и «Дредноутов», удостоен, например, «Золотой маски» в двух номинациях.

Вроде бы два очень разных человека. Но оба они сейчас покажут, как надо быть обычными людьми. Это вообще очень интересный момент: на планете шесть миллиардов человек, но есть среди них несколько десятков тысяч, которые очень существенно меняют мир вокруг... Или только так кажется, что они что-то меняют. Вот представьте себе параллельную вселенную без Вирта. Какими были бы современные языки программирования? (кстати, раз сегодня день информатики, то рекомендую короткий анекдот на эту тему :)

Ну да речь не о том. Так сложилась жизнь, что я пообщался живьём и с Виртом, и с Гришковцом. Кстати, хозяйке на заметку: не очень весело толпиться в очереди до гардероба после спектакля - можно чуть-чуть задержаться в зале, чтобы в спокойной обстановке поговорить с интересным человеком.

В разговоре выясняется, что они «совершенно обычные люди». Это важно прочувствовать. В современном мире выражение «обычный человек» имеет негативный окрас. Но живой разговор с очень известными представителями человечества ставит всё на свои места. Иногда вахтёры, бухгалтеры и кассиры сберкасс ведут себя не как обычные люди, всем своим видом показывая свою важность и особенность. Но с Виртом и Гришковцом всё не так.

Быть обычным человеком - это разрабатывать концепции, определяющие развитие компьютерных технологий на десятилетия вперёд, интересно писать тексты и хорошо играть на сцене. У меня была небольшая переписка с Евгением Рошалом (его знают почти все по архиватору RAR и файловому менеджеру FAR) и Леонидом Кагановым. Подозреваю, что разработками первого пользуется даже больше людей, чем знающих о существовании второго. Ну да речь не об этом, а о том, что в переписке они выглядели совершенно обычными людьми.

Выясняется, что вполне можно делать важные и серьёзные вещи, менять жизнь большого количества людей, оставаясь открытым и «нормальным» человеком.

Будьте обычными людьми. Меняйте мир к лучшему.

Правила для бесправия

А иногда попадаются на глаза совсем странные новости (цитата): «Посольство Франции в Москве отказалось выдать визы членам сборных России по борьбе, планировавшим принять участие в турнире имени Анри Деглана, который пройдет 27 и 28 ноября в Ницце. По словам первого вице-президента Федерации спортивной борьбы России (ФСБР) Георгия Брюсова, французская сторона не назвала причины своего решения.»

Разгадка этого ребуса будет позже, а пока давайте вникнем в требования для получения визы. Например, необходимо предоставить две фотографии размером 35 на 45 миллиметров, сделанные таким образом, чтобы размер головы от макушки до подбородка составлял около 3 см, а изображение лица занимало около 70-80% фотографии. Бывают ли такие фотографии лиц?

Рассчитать легко: площадь фотографии - 3.5х4.5=15.75 сантиметров квадратных. А лицо должно занять от 70 до 80 процентов этой площади. Считаем: 15.75х0.7=11.025. Другими словами, чтобы удовлетворить требованию «лицо занимает 70% фотографии», необходимо иметь площадь лица более 11 квадратных сантиметров. Но в этих же требованиях сказано, что высота лица всего 3 сантиметра.

Получается, что лицо обязательно должно быть очень широким. Даже о-о-очень широким! На «исправленной» фотографии справа можно видеть, что даже если расстояние от уха до уха совпадёт с шириной фотографии, то площадь лица всё равно будет меньше половины площади фотографии. И легко понять, с чем это связано: лицо больше похоже на эллипс, а не на прямоугольник, поэтому у него остаются «пустые» углы по краям.

Если бы лицо было идеальным прямоугольником, то его площадь составила бы 3х3.5=10.5 квадратных сантиметров. Это почти то, что требуется, но всё ещё чуть-чуть не хватает для достижения цели хотя бы в 70%. Выходит, мало иметь широкое и прямоугольное лицо! Что же делать? Есть один выход - надо отрастит щёки и уши - они бы свисали и торчали по краям, позволяя удовлетворять странным требованиям :)

Вообще говоря, такие ограничения на фотографии позволяют не выдавать визу любому человеку. И не из-за каких-то «политических соображений», а по простейшей причине - «не смог правильно подать документы». Соменевающиеся в том, что требования к фотографиям именно такие, легко могут снять все вопросы, зайдя на официальные сайты консульств (или спросив у поисковых систем «Изображение лица должно составлять около 70-80 % фотографии»). Это очень распространённое требование, которое совершенно не совместимо с остальными ограничениями.

И система работает (выдаёт визы) только по одной причине - сотрудники посольств не выполняют свои же правила. Кстати, это не очень хорошая практика. Но она показывает, что даже государственные организации иногда работают адекватнее, чем некоторые коммерческие банки. Впрочем, тот факт, что бюрократическая машина много лет не может убрать противоречивость из правил, а заставляет работников эту ошибку игнорировать, показывает крайне низкую скорость системы.

Ну а что же было с нашей сборной по борьбе? Если верить тем же журналистам, всё не совсем так плохо: «Советник посольства по делам прессы Том Бюффен заявил, что некоторые члены российской делегации не подали все нужные документы», а «основная часть команды получает въездные визы во Францию в четверг, 26 ноября». Складывается впечатление, что журналисты переврали слова вице-президента Федерации спортивной борьбы или он не очень точно выразился.

А какие примеры подобных массовых нарушений своих правил вы знаете?

Хороших вам выходных!

Правила ради правил

Расскажу сегодня забавную историю, которую на днях наблюдал. Она ярко показывает осмысленность правил ради правил (особенно, если система так устроена, что все их соблюдают), а также лишний раз подтверждает тезис о том, что нет никакого кризиса :)

Итак, приходит мой знакомый с неожиданно свалившимся на него чемоданом денег (наследство получил) в Альфа-банк, чтобы сделать вклад, так как столько денег прямо сейчас ему не надо. И через час консультаций со специалистами и стояния в очередях (ну да, не так всё быстро в нынешнем мире), он выясняет, что деньги у него принять не могут.

Вы вообще можете себе представить ситуацию, чтобы банк не стал срочно заключать договор с человеком, который уже пришёл и на всё согласен? Оказывается, это бывает. И по очень неожиданной причине.

Заинтригованы? Оказывается, проблема в том, что данный человек уже однажды пользовался услугами этого банка. У него осталась карточка Виза-Электрон, на которой уже много лет почти нет денег. Это преступление? Нет, за это банк ничего не сделает. А вот тот факт, что карточку он получил до того, как сменил гражданство - реальная проблема.

Ему не могут открыть вклад на новый паспорт, потому что он уже клиент банка - должен пользоваться тем документом, по которому начал. Чтобы открыть вклад, он должен закрыть договор по старой карточке. Для этого необходимо произвести её перевыпуск на новый паспорт - это несколько дней возни. И только после этого можно будет делать что-то новое. И открыть вклад на новый паспорт они не могут, потому что не должно быть две разных записи в базе данных для одной персоны. Я не банковский работник, поэтому не уверен, что правильно понял пересказ их объяснений. Возможно, всё было чуть-чуть иначе.

Короче, потерял он час времени, чтобы в результате выяснить, что обслужить его не могут. И ушёл, естественно, в другой банк. Потому что у него уже плохие ассоциации с этим. Да и нет желания рисковать, храня кучи наличности дома, пока банк изыскивает возможность как-то принять её.

Как и в заметке смысл в бессмысленности, мы сталкиваемся с непродуманными правилами, за соблюдением которых жёстко следят. Виноваты ли сотрудники банка? Скорее всего, у них не было выбора. Виноваты те, кто им этого выбора не оставил - авторы негибкой системы. Сколько ещё клиентов не получила их организация из-за подобных бюрократических глупостей?..

Поэтому вопрос: с какими похожими глупостями вы сталкивались в своей жизни?

Хорошей вам недели!

Перепроизводство и подарки

Во многих умных экономических книжках написано, что банкротства - это совершенно нормальные и правильные явления, потому что они убирают с рынка тех, кто больше не нужен. Остаётся только понять, откуда берутся эти компании, чьи услуги/товары перестают покупать...

Рассмотрим, например, наручные часы. У меня есть четыре экземпляра электронных часов: одни я купил лет 15 назад, а ещё трое часов были подарены родственниками и друзьями. Все они прекрасно работают, но чтобы это состояние сохранилось, из них давно извлечены батарейки. Ещё есть пара механических часов - память о дедушках. Но все эти часы я не ношу, так как уже давно привык к мобильному телефону. И у многих моих знакомых тоже есть хотя бы 3-4 экземпляра различных часов. И с возрастом их количество только растёт.

Понятно, что мобильные телефоны нанесли удар по рынку наручных часов. Но ежу же понятно, что если у меня и так есть 6 штук, то нет резона покупать седьмые. Поэтому я не смог бы поддержать производителей часов даже без современной распространённости мобильных телефонов.

Интереснее другое - слишком много предпринимателей решили направить свои ресурсы в это производство. Видя интенсивность, с которой часы раскупают, они решили, что так будет всегда: настроили заводов, наняли людей, работа закипела. И рынок мгновенно насытился. А теперь работники тех заводов не могут найти новое занятие, чтобы кормить своих детей. Почему у них много детей? А они видели много рабочих мест вокруг, поэтому были уверены, что всегда смогут заработать.

Сейчас часто можно услышать призывы нарастить потребление, чтобы спасти реальный сектор экономики. Мол, надо раздать населению кредиты, тогда люди пойдут покупать, заводы оживут, их работники получат зарплату, поэтому смогут выплачивать проценты по ранее взятым кредитам. Но мы сейчас имеем очень сильные несбалансированности в экономике планеты: масса людей занимается тем, что человечеству не нужно. И если удастся продолжить их поддержку, то на следующей итерации производителей мусора станет ещё больше, а на их спасение потребуется ещё больше сил. Впрочем, про природу кризиса мы уже говорили год назад.

Я это так вижу: большая масса людей в один момент кидается что-то скупать, поэтому бизнес изыскивает возможность данный товар произвести. На следующей итерации люди уже не хотят тот товар, но производство налажено, поэтому активно включаются рекламисты, чтобы продлить жизнь предприятий, поддерживая продажи их ненужного барахла. Тут же отрабатывают свой хлеб кредитные институты, зазывающие людей приобрести дорогие и ненужные вещи...

Давайте посмотрим на деятельность человечества со стороны: мы добываем полезные ископаемые, чтобы произвести нечто, а потом отправляем это на свалку. Очевидно, что если во многих квартирах планеты количество часов превышает количество людей в несколько раз, то их производили слишком много. И это касается почти каждой группы товаров :(

Многолетние традиции не позволяют прийти без подарка большому количеству людей. Поэтому до визита к друзьям или родственникам многие идут в торговый центр. А там их уже ждут специальные впариватели барахла, умеющие предложить ненужные, но соответствующие поводу вещи для любого бюджета.

Поэтому опрос:

1. Есть ли у вас родственники, периодически дарящие одежду, которая вам не подходит? Или из-за фасона, или размер не тот, или качество не устраивает, но их подарок вы надеваете только один раз - примерили при дарителях «чтобы порадовались».

2. С какими дурными проявлениями подарков, сделанных «потому что нельзя прийти с пустыми руками» вы сталкивались? Удавалось ли убедить своих друзей/родственников больше так не делать?

3. Сколько у вас наручных часов?

Транзитивность

Добрый день.

В недавней заметке о разборчивой невесте мы рассматривали группу кандидатов, между которыми есть транзитивное отношение. Записывали мы это так: если А лучше Б, а Б лучше В, то А заведомо лучше В для произвольных A, Б и В. При выполнении этого условия для любой тройки кандидатов можно говорить, что отношение «лучше» является транзитивным.

Например, отношение «тяжелее» тоже является транзитивным: если А тяжелее Б, который тяжелее В, то А тяжелее В. С числами тоже всё легко: если a>b и b>c, то a>c. Легко показать, что свойства параллельности прямых или делимости чисел являются транзитивными.

А отношение дружбы уже может не быть транзитивным: иногда бывает так, что одному и тому же человеку рады в двух воинствующих компаниях. Отношение «коллега» тоже не обязано быть транзитивным: если А и Б работают в одной организации, а Б и В тоже работают в одной организации, то это не значит, что А и В коллеги, так как Б может успевать работать в двух разных местах. Отношение любви вообще не является транзитивным: если А любит Б, а Б любит В, то, скорее всего, А испытывает к В неприязнь.

Итак, мы знаем, что не все отношения являются транзитивными, но иногда попадаем в ловушку собственной интуиции. В комментариях к прошлой задачке о трёх шестигранных костях звучала идея о том, что если первый кубик выигрывает чаще второго, а второй - чаще третьего, то первый должен выигрывать чаще третьего. В это хочется поверить, но легко убедиться в том, что это всего лишь иллюзия.

Но сначала давайте поймём, как вообще можно считать вероятность того, что одна кость выиграет другую. Предлагаю доверить это дело компьютеру (кстати, это неплохая задачка для освоения его возможностей): запускаем любой табличный процессор и записываем в него строчку и столбец из 6 чисел - значения на гранях первого и второго кубиков, соответственно. В образовавшееся поле 6 на 6 клеток поставим статусы «победил»/«проиграл» (я ставил 1 и 0, чтобы было проще считать). Для этого я записал формулу в верхнюю левую ячейку таблицы, которая для каждой из 36 ячеек сравнивает самое левое число (с грани одного кубика) с самым верхним (с грани второго кубика) - моя формула видна в верхнем правом углу изображений. А потом просто «растянул» эту ячейку на оставшиеся 35 клеток, чтобы получить результаты для всех возможных состояний.

Что мы получили? Сейчас поймём! Один кубик может выпасть шестью разными способами. Второй - тоже шестью способами. Поскольку кубики друг на друга не влияют, то есть 36 разных равновероятных вариантов состояний пары кубиков после броска. Вот мы и рассмотрели все эти 36 вариантов. Остаётся просуммировать единички в таблице, чтобы увидеть, что кубик, значения граней которого расположены вертикально, побеждает в 21 случае из 36. Это значит, что с вероятностью примерно 58% кость (2 3 4 15 16 17) окажется сильнее кости (1 8 10 11 13 14).

Научившись точно определять вероятность победы одного кубика, мы можем рассмотреть разные наборы из трёх кубиков. Например, в комментариях был предложен набор, в котором первый кубик сильнее второго, второй - сильнее третьего, а третий - сильнее первого. Другими словами, какой бы кубик ни оказался у нашего соперника, мы всегда можем выбрать из оставшихся двух такой, который будет чаще побеждать. Прекрасная аналогия на эту тему - игра «камень-ножницы-бумага». В ней нет самого сильного хода, так как каждый вариант проигрывает одному, но выигрывает другого.

Мне кажется, самое сложное в этой задачке - сопротивление интуиции. Не так сложно найти набор из трёх кубиков, для которых отношение «сильнее» не является транзитивным (как мы убедились выше, легко реализовать перебор на компьютере). Сложнее догадаться, что такой набор костей существует :)

Другими словами, побеждает тот, кто размещает числа на кубиках, а не тот, кто выбирает любой из трёх кубиков, как многим кажется. Напишите, пожалуйста, с какими случаями иллюзии транзитивности вы сталкивались. Бывают не только математические задачки, но и вполне жизненные ситуации - интересны и те, и другие.

Хорошей вам недели!

Клад и кости

Добрый день.

Сегодня я хочу напомнить одну старинную задачу о честном дележе клада, а потом предложу игру, чем-то похожую по постановке, но очень отличающуюcя по сути.

Если два пирата нашли клад, но не считают правильным расправляться друг с другом, чтобы единолично им завладеть, то есть один хороший выход - честно его поделить. Осталось придумать, как бы так распределить добычу, чтобы оба были довольны. Уже не один век известен следующий алгоритм:
1. Один участник делит весь клад на две части, после чего отходит в сторонку.
2. Второй, внимательно изучив две кучи всевозможных ценностей, выбирает себе одну из них.
3. Соответственно, первому остаётся то, что второй не забрал.

Тогда у обоих пиратов прослеживаются простые и ясные цели: первый хочет разделить весь клад на равные по ценности группы, а второй имеет возможность выбрать из них более ценную, если первый попытается схитрить.

Существует естественное расширение этой задачи на группу из более чем двух пиратов, но сейчас мы не будем разбираться с этой интересной проблемой, а перейдём к игре, в которой игроки тоже поочереди подходят к игровому столу, имея возможность чуть-чуть менять снаряды и выбирать их себе для следующего хода.

Но сначала вспомним, что в прошлом году мы уже изучали вопрос «какой шахматист лучше?». Если у нас есть несколько признаков, то не так легко разобраться, какой из них важнее, поэтому задача не такая простая (и порождает массу споров). Проблема стояла серьёзная, поэтому я опубликовал вариант решения. Но суть коротко напомню здесь: тонкость была в том, что до игры в правилах не было чётко сформулировано, что значит «один шахматист лучше другого». А если нет правил, то можно выдумывать сколь угодно красивые аргументы. Поэтому и могли возникать горячие споры, в которых невозможно победить.

Теперь, имея этот опыт, мы будем определять правила предельно ясно ;)

Итак, есть 3 шестигранных игральных кости с чистыми гранями и один маркер. Двое игроков действуют следующим образом:
1. Первый рисует на гранях костей числа от 1 до 18 (без повторов, поэтому использует все 18 чисел на всех 18-ти гранях).
2. Второй выбирает себе одну из трёх игральных костей.
3. Первый выбирает одну из двух оставшихся.
4. После этого игроки бросают свои кости - выигрывает тот, на чьём кубике выпадет большее число.

Вопрос: кто будет чаще выигрывать при правильных действиях обоих игроков? Решая задачу, надо исходить из того, что игра честная, а оба участника хотят выигрывать как можно чаще.

Приглашаю обсудить эту задачку в комментариях. Хороших вам выходных!

Проблема остановки выбора (разборчивая невеста)

Знаете ли вы, что 33% студенток Гарвардского университета вышли замуж за своих преподавателей в 1901 году? Можно представить себе, что написала бы жёлтая пресса про учителей вроде бы приличного ВУЗа, которые не умеют себя контролировать... Впрочем, если разобраться, то окажется, что в том году в Гарварде было всего три студентки, одна из которых вышла замуж за своего профессора. Утверждение может быть абсолютно корректным, но выглядеть дико, если его «удачно» подать. Поэтому знание математики необходимо обществу, если оно не хочет слепо следовать за первым попавшимся жуликом.

Разберём коротко прошлую задачку о странном любовном треугльнике: Женатый Джек любит Анну, которая влюблена в холостого Джорджа. Вроде бы мы не знаем статус Анны, но давайте рассмотрим оба варианта:
- Если Анна состоит в браке, то она и есть тот человек, который любит холостого.
- Если Анна свободна, то женатый Джек является тем человеком, который любит незамужнюю.
Это означает, что ответ «недостаточно данных» является преждевременным. Похоже, интуиция многим мешает разобрать обе возможные ветки этой задачи. Я тоже чуть было так не ответил, но вовремя сообразил, что «не зря же мне эту задачу предложили». И тогда подумал ещё раз, что и привело к полному пониманию ситуации.

Задача очень простая, но, судя по всему, редкий человек успевает заставить себя подумать второй раз... Это очень интересный эффект, мне кажется. Его интересно прочувствовать на себе, чтобы быть внимательнее в жизненно важных ситуациях.

Раз у нас нынче идёт неделя вероятностей, женитьб и чисел вида 1/e (речь о парадоксе с раздачей подарков), то имеет смысл вспомнить ещё одну задачку, которая возникла совсем недавно - буквально 50 лет назад. Мы её знаем как задачу о разборчивой невесте или проблему остановки выбора, а зарубежом она обычно называется «secretary problem» или «marriage problem» (конечно, есть ещё масса названий).

Проблема формулируется так:
- есть множество из N претендентов на одну вакансию/руку принцессы;
- про любых двух претендентов есть надёжный способ определить, какой из них лучше (более того, если А лучше Б, а Б лучше В, то А заведомо лучше В);
- наниматель/принцесса общается с претендентами в случайном порядке;
- с каждым претендентом можно поступить одним из двух способов: согласиться (тогда игра заканчивается), отказать ему (но тогда он больше не вернётся, поэтому уже никогда нельзя будет принять его предложение);

Цель нанимателя/принцессы: выбрать самого лучшего из возможных.
Вопрос: как следует действовать и с какой вероятностью цель будет достигнута?

В чём проблема? А в том, что если принцесса отказала всем, кроме одного, то ей придётся за него выйти. Поэтому слишком большая разборчивость может привести к тому, что она упустит своего самого лучшего принца. Но если она согласится слишком рано, то даже не позволит чемпиону проявить себя. Надо знать меру, но как её найти?

Оказывается, правильная стратегия состоит в следующем:
1. Делим всех N претендентов на две группы: «эксперементальная» (1/e от всех) и «рабочая» (1-1/e от всех).
2. Первой группе (первым N/e претендентам) следует отказать, запоминая, кто из них самый лучший.
3. Представители второй группы уже имеют шансы: следует соглашаться на предложение первого же, кто лучше всех своих предшественников.

Интересно, что при этой стратегии принцесса получит наилучшего принца с вероятностью 1/e (согласитесь, не так уж и мало, учитывая сложность ситуации). Эта задача имеет интересные расширения. Например, если принцесса не слишком привередлива, то она может прожить счастливую жизнь не с самым лучшим принцем, а с тем, кто входит в список «k лучших принцев». Если k=2 (если принцесса согласна на любого из двух самых лучших), то при правильной стратегии она найдёт своего принца с вероятностью 57 процентов.

Рекомендую прочитать интереснейшую книгу на эту тему - Разборчивая невеста (всего 200 килобайт). Это 25-ый выпуск библиотеки «Математическое просвещение» - на двух десятках страниц изложены очень интересные подходы к решению задач (кстати, многие школьники вполне смогут понять этот материал, поэтому стоит попробовать им предложить!). Любители английского языка и противники pdf-файлов найдут статью в википедии (не так подробно, но есть ссылки на близкие по содержанию материалы)

Хорошего дня!

Замуж за иностранца

Иногда возникает ощущение, что люди делают так, чтобы им было лучше. Это простая и естественная формулировка, которая привычно пропускает один важный момент. Люди стараются сделать так, как им кажется будет лучше. И иногда им кажется правильно.

Недавно мы говорили о резком и случайном изменении всех жизненных планов, об ощущении потери шансов на что-то важное из-за какой-то ерунды. Часто это чувство связано с тем, что мы не имеем (и не можем иметь) точного представления о том, как поменялось наше будущее в результате данного конкретного локального действия. Впрочем, через некоторое время вполне возможно согласие с такими изменениями, потому что может созреть понимание, что имело место очень даже удачное стечение обстоятельств.

Давайте попробуем разобраться в такой ситуации, где не очень ясно, что известно, а что неизвестно. Возьмём для примера женатых и холостых иностранцев, которые женились друг на друге и повыходили замуж, а теперь имеют всякие хитрые взаимоотношения. Эту забавную задачку я узнал из комментария к недавней заметке об IQ тесте:

Джек женат, но любит Анну, которая влюблена в холостого Джорджа. Верно ли, что человек, состоящий в браке, любит человека, в браке не состоящего?

Варианты ответа: «Да, это так», «Нет, это не так», «Мало данных для точного ответа», «Я уже видел эту задачку, поэтому знаю ответ». Пожалуйста, оставьте своё мнение в комментариях к заметке, не читая чужих версий.

Скорее всего, в одной из следующих заметок мы разберёмся с этой задачей, а пока я предлагаю вернуться к парадоксу раздачи подарков. Поскольку меня попросили рассказать, как найти точное решение, а изложить его в комментариях не очень легко, так как оно достаточно объёмное, то посвятим этому делу вторую половину сегодняшней заметки.

Если вам не очень интересно читать длинные и подробные математические рассуждения, то предлагаю прочесть только подведение итогов - от абзаца, начинающегося словами «Уф-ф...» :)

Сразу предупрежу, что ниже предложен не самый короткий путь, потому что у меня нет цели быстро доказать, что данная формула верна. Главная задача - показать, как до неё можно дойти. Я привожу ход мыслей, который кому-то покажется корявым, а кому-то понятным, потому что все люди разные. Надеюсь, желающие смогут прорваться сквозь лишние подробности.

Итак, есть N подарков и N людей, каждый из которых получит ровно один подарок. Это значит, что есть ровно N! способов раздать подарки этим людям (первый получает один из N подарков, второй - один из (N-1) оставшихся подарков, третьему достанется один из (N-2) подарков и так далее). Перемножаем все эти независимые случаи, получаем N*(N-1)*(N-2)*(N-3)*...*2. Запомним этот результат, он нам много раз пригодится.

Теперь давайте разберём случай, в котором первый человек уже получил свой подарок. Это значит, что у нас осталось (N-1) людей и (N-1) подарков (причём каждый подарок принёс один из этих оставшихся). Сколькими способами они могут распределить эти подарки между собой? Как мы установили в предыдущем абзаце, есть (N-1)! способов. Давайте это запомним: если один человек получил свой же подарок, то остальные (N-1) человек могут распределить между собой подарки (N-1)! способами.

Теперь рассмотрим ситуацию, когда второй человек получил свой подарок. Оставшиеся опять могут распределить подарки X1=(N-1)! способами. Аналогично для третьего, четвёртого,... , N-ного участника. Получается, что если сложить все эти случаи, то выйдет N*X1=N*(N-1)!, что как раз равно Y1=N!. Пока всё просто, но сейчас надо осознать одну важную вещь: некоторые возможные ситуации были посчитаны несколько раз. В самом деле, случай, когда первый и второй участники одновременно получили свои подарки, учтён дважды (в первой и во второй сумме). Поэтому для получения правильного ответа необходимо из нашего результата Y1=N! один раз вычесть дважды учтённые расклады (для парных совпадений). Более того, в этот Y1=N! случаев трижды включены расклады, в которых первый, второй и третий участники одновременно получили свои подарки на руки. Такие случаи тройных совпадений надо вычесть дважды (чтобы осталось ровно одно). Дальше аналогично: четвёрки посчитаны по четыре раза, их надо вычесть трижды, пятёрки посчитаны пять раз - их надо вычесть четыре раза. И так далее. Звучит сложно, но мы вот-вот доберёмся до результата.

Давайте разберём случай, в котором двое участников получили свои подарки на руки. Оставшиеся (N-2) участника, как мы выяснили недавно, могут распределить оставшиеся (N-2) подарка ровно X2=(N-2)! способами. Выходит, надо просуммировать все эти X2 конфигурации для всех возможных пар из N участников. А таких пар может быть ровно N*(N-1)/2! (потому что порядок не имеет значения). Выходит, что таких конфигураций ровно N*(N-1)/2 * X2, что как раз равно Y2=N!/2.

Опять важно отметить, что мы несколько раз посчитали одинаковые конфигурации: например, случай, когда первый, второй и третий участники одновременно получили свои подарки, учтён 3 раза. Поэтому для получения правильного ответа из нашего результата Y2=N!/2 необходимо два раза вычесть трижды учтённые расклады. Аналогично - для четвёрок, пятёрок и так далее.

Для ясности рассмотрим следующий шаг: считаем, сколько возможно случаев, в которых трое получили свои подарки. Поскольку трёх человек из N можно выбрать N*(N-1)*(N-2)/3! способами, то получаем результат N*(N-1)*(N-2)/6, что равно Y3=N!/6. Но опять же в нём посчитаны лишние четвёрки, пятёрки... Их тоже надо будет вычесть.

Соберём получившийся «хаос»: заметим, что выражение T(N)=Y1-(Y2-(Y3-(Y4-(Y5-...)))) нам очень удобно. Оно как раз обладает замечательным свойством: многократно учтённые случаи благополучно вычитаются нужное количество раз, поэтому все возможные расклады остаются в количестве ровно одной штуки (надо посмотреть на эту строчку несколько десятков секунд, чтобы почувствовать это). Другими словами, T(N) - это как раз и есть идеальный ответ. T(N) - это количество ситуаций без повторов, в которых хотя бы один участник получил свой подарок обратно. Если из общего количества возможных раскладов N! вычесть T(N), то мы получим количество случаев, в которых никто не получил свой подарок обратно.

Подставим Yi в формулу и раскроем скобки: выходит T(N)=N!-(N!/2!-(N!/3!-(N!/4!-...)))=N!-N!/2!+N!/3!-N!/4!+N!/5!-...-(-1)^N.

Теперь найдём Z(N) - количество ситуаций, в которых каждый получил чужой подарок: Z(N)=N!-T(N)=N!/2!-N!/3!+N!/4!-N!/5!+...+(-1)^N.

Ну а теперь найдём P(N) - вероятность того, что никто не получит свой подарок обратно. Для этого надо разделить количество интересных нам элементарных исходов на количество всех возможных элементарных исходов N!.

P(N)=Z(N)/N! = 1/2! - 1/3! + 1/4! - 1/5! + ... + (-1)^N/N!.

Уф-ф... Длинно вышло. Поздравляю всех дочитавших до этого места :)
Если хотите предложить более короткое и ясное решение, то это будет очень интересно! Приглашаю в комментарии к заметке, посвящённой задачке о подарках. Вопросы о данном решении, пожалуйста, задавайте там же.

Ну а тот факт, что P(N) стремится к 1/e при N стремящемся к бесконечности, легко понять, так как разложение в ряд Тейлора функции экспонента как раз совпадает с P(N) при параметре -1 (exp(-1)=Sum{k=0..inf}(-1)^k/k!). Интересно вот что: P(N) стремится к 1/e очень быстро. Уже для семи участников P(N) приблизительно равно 0.3679 (то есть, совпадает с 1/e с точностью до четырёх знаков после запятой). Мне кажется, это вообще очень важно осознать: если вероятность каждого конкретного события всего лишь 1/N, но этих событий N штук, то вероятность того, что хотя бы одно произойдёт, получается около 2/3. То есть, хотя бы одно событие скорее произойдёт, чем ничего не произойдёт.

Если вам эта тема показалось такой интересной, что хочется прочитать ещё что-то, то рекомендую поискать статьи с распределением Пуассона в главной роли (сейчас мы рассматривали распределение с параметром λ=1). Оно известно человечеству с 1837 года - тогда Симеон Денис Пуассон издал книгу со своими размышлениями о различных последовательностях испытаний Бернулли. В то время эти исследования не нашли себе применения, но после 1894 года распределение Пуассона пригодилось при изучении одного странного феномена: германская армия анализировала статистику трагических случаев, когда солдат был убит ударом копыта. Согласно наблюдениям, 196 солдат погибли таким образом за 280 наблюдений (20 лет умножить на 14 кавалерийских корпусов). Это значит, что можно ожидать, что события будут подчинены распределению Пуассона с параметром λ=0.7. Другими словами, должно было быть 139 случаев без смерти участника, 97 наблюдений с одной смертью, 34 наблюдения с двумя смертями и так далее. Реальность оказалось такой: 140 случаев без жертв, в 91 случае был один убытый копытом, в 32 случаях - двое. Реальные наблюдения очень хорошо совпали с теоретическими размышлениями, что очень поддержало теоретиков, хотя солдат, конечно, жалко.

В реальной жизни мы сталкиваемся с распределением Пуассона почти везде. Например, если N - количество доступных телефонных линий, то число занятых линий приблизительно подчинено распределению Пуассона. Это распределение всюду вокруг нас, поэтому бывает полезно примерно понимать его природу :)

Напишите, пожалуйста, свой ответ о женатых иностранцах и замужних иностранках в комментариях, если ещё этого не сделали.

Хорошей вам недели!

Вероятности и подарки

Скоро Новый год и ещё неделя праздников, скоро масса подарков и встреч хороших людей. В это время в голову приходят идеи всяких праздничных игр. В некоторых группах принято делать так: все кладут по одному подарку под ёлку, нумеруя их, а потом для каждого участника выбирают номер подарка, который он сейчас получит (обычно пользуются компьютерным генератором псевдослучайных чисел). Это добавляет ситуации загадочности и праздничности :)

Какие рассуждения при этом используются?

Если у нас N участников и N подарков, то вероятность того, что лично мне достанется тот же подарок, что я положил под ёлку, равна 1/N (и это же можно сказать про остальных людей). Чем больше N, тем меньше вероятность вытянуть своё же (и при N стремящемся к бесконечности эта вероятность вообще стремится к нулю). Поэтому в больших группах очень мало шансов, что кто-то уйдёт со своим же подарком.

Недавно мы уже говорили о том, что словами «бесконечность» и «предел» нужно пользоваться очень осторожно, чтобы не обмануть самого себя. А про любые «очевидные» логические переходы надо уметь в течение 30 секунд детально и корректно объяснить, почему они очевидны. Но сегодня я предлагаю начать с обратной стороны: поставить эксперимент.

Проще всего для этого воспользоваться языком программирования javascript, потому что он есть под рукой почти у всех читателей (да и традицию не будем нарушать). Создайте файл presents.html со следующим содержимым и откройте его браузером:

<script type="text/javascript">
N = 100;     // quantity of presents (and participants)
nbIt = 1000; // quantity of iterations
okIt = 0;    // OK situaions
for (iter = 0; iter < nbIt; iter++) {
  var a = new Array(N); // create array
  for(i=0; i<N; i++)
    a[i] = i; // fill it by numbers 0, 1, 2,... , N-1

  // shuffle array
  i = N;
  while(i) {
   j = Math.floor( (i--) * Math.random() );
   t = a[i];
   a[i] = a[j];
   a[j] = t;
  }

  // calculate number of self-presents
  selfp = 0;
  for(i=0; i<N; i++)
    if (a[i] == i)
      selfp++;

  if (selfp == 0) // if there are no self-presents
    okIt++;       // increase OK-counter
}

document.write('Probability of OK-situation: ' + (100*okIt/nbIt) + '%');
</script>

Данная программа реализует следующий эксперимент: сто участников складывают принесённые с собой подарки под ёлку, а потом получают на руки случайный подарок. Если никому не досталось то, что он принёс своими руками, то считаем ситуацию хорошей. Один раз так делать смысла нет, поэтому ребята повторяют это тысячу раз, считая хорошие ситуации. Последней строкой программа выводит долю случаев, в которых никто не получил свой подарок.

Оказывается, что только примерно в трети случаев каждый участник эксперимента получает что-то новое, а в остальных ситуациях кто-то оказывается не очень довольным. Попробуйте увеличить или уменьшить количество участников (конечно, не делая его слишком малым - больше 5 уже достаточно). Результат всё равно будет больше похож на температуру (потом мы поймём, что он колышется вокруг 36.8%).

Давайте отметим этот момент: вроде бы было очевидно, что в большинстве случаев на больших группах людей все будут довольны. Но эксперимент надёжно показал, что примерно в двух третях всех случаев кто-то получит обратно собственноручно принесённый подарок. Данный пример лучше ранее рассмотренной задачи о двух конвертах, потому что легко сочинить корректный эксперимент, с результатами которого трудно спорить.

Зачем это надо? Для калибровки своей интуиции! Редкий человек обладает достаточной дисциплиной ума, чтобы проверять каждый шаг всех выкладок. Иногда приходится полагаться на ощущение «это верное утверждение, потому что оно не может быть ошибочным»... Но чтобы чего-нибудь достичь, позволяя себе такие вольности, необходима тренированная интуиция, а не умение переспорить. Эти глубокие интуитивные шаги необходимы, чтобы не погрязать в рутине маленьких простых этапиков в размышлениях, а сразу выделять важные и серьёзные идеи (которые потом, конечно, надо будет детально обосновать, если они покажутся интересными).

Полагаю, скоро в комментариях появится объяснение, почему даже для небольших групп людей вероятность получения сюрприза каждым не очень высока. А самое интересное, почему эта вероятность не устремляется к 100% при росте количества участников :)

Манипуляции полезны?

Иногда крайне трудно объяснить человеку честно и коротко, почему что-то делать нельзя (или необходимо). Например, если образование слушателя не позволяет ему понять современное научное представление о ситуации, то порой лучше слегка «сократить сказочку», чтобы её дослушали и приняли к сведению. Сообщение должно учитывать условия его получения! Порой просто нет времени и ресурсов для ясного и правдивого изложения.

Сейчас уже можно кидаться камнями с надписью «и ты тоже о свином гриппе», но я попробую успеть до этого сказать, что пример с ним будет короткий (один последний абзац), а сама заметка о другом.

Теоретический вопрос состоит в следующем: допустим ли небольшой обман, если от этого зависят тысячи жизней? Кто-то ответит, что недопустим. Увы, сейчас это почти никого не интересует, потому что стало очень обычным. Недавно мы вспоминали очень распространённое различие в представлениях о названии романа Льва Толстого «Война и мир». Как вы понимаете, такой миф существует не для спасения в критической ситуации. Полагаю, он так хорошо живёт из-за того, что «массирует чувство собственной важности» - приятно ощущать себя понимающим глубину великой литературы.

Итак, вооружившись идеей о двух позициях (массовой и осмысленной), давайте разберём какой-нибудь пример очень распространённого представления, чтобы найти в нём общечеловеческий смысл (а не только происки аптекарей или ещё кого-нибудь). А потом попробуем понять, правильно ли поддерживать такое распространённое представление.

Вспомним, например, что человечество пока не умеет надёжно лечить ВИЧ-инфицированных, а их количество продолжает расти. Самые эффективные и частые способы передачи ВИЧ - использование общего шприца для инъекций и анальный секс (заразиться при традиционном значительно труднее, если верить официальной статистике). А раз так, то массовое неприятие наркоманов и гомосексуалистов может быть вполне позитивным явлением для здоровья человечества.

Почему многие ненавидят наркоманов? Объяснения какие-то такие: из-за них высокая преступность (хотя мне одинаково неприятно сталкиваться на улице с группой наркоманов, группой алкоголиков, психически нездоровым человеком, агрессивной бродячей собакой и так далее, так как все они могут опасно атаковать), они не приносят пользы человечеству (сколько вполне здоровых людей сидит на пособиях, ничего не делая для остальных, а только потребляя чужие достижения?), они своей беспутной жизнью угнетают родственников и друзей (как и вполне разрешённые и воспеваемые фольклором алкоголики). Подобных аргументов большинству вполне достаточно, чтобы не поддерживать наркоманов (и есть аналогичные по убедительности соображения против гомосексуалистов).

Можно долго спорить о том, хорошо это или плохо, что распространено неприятие к двум данным категориям граждан. Но сам факт этого неприятия, возможно, останавливает какую-то группу ещё здоровых людей от действий, приводящих с большой вероятностью к ВИЧ-инфицированию. И если это работает (данных у меня нет), то, возможно, не так это и плохо?

Про тот же алкоголь есть теория, что многие из страшных данных о потреблении спирта в России серьёзно завышены, чтобы создать иллюзию и правильно настроить большую часть общества. Представьте, что ради сокращения смертности от пьянства, умные люди громко рассказывают об огромных потерях (например, из-за отравления «палёной» водкой). СМИ что угодно радостно тиражируют, а впечатлительный человек может решить поберечься, «раз все вокруг так мрут»... Купит чуть меньший объём, но не по самой низкой цене и не в самом грязном подвале. Опять же, можно спорить об эффективности таких мер, но интересно понимать саму эту возможность (да, я оптимист).

Или давайте поймём возможный смысл истерики с тем же свиным гриппом. Чего боятся некоторые биологи? Вроде бы ничего выдающегося в новом штамме нет - смертность от него и способность распространяться вполне рядовые. А какую пользу тогда может приносить массовая паника (речь сейчас не об экономической выгоде отдельных участников рынка)? Есть теория, что последние годы один из основных рисков - одновременное заражение человеческой клетки «птичьим гриппом» и любым штаммом «обычного» гриппа (в том числе, и «свиного»). При этом с некоторой вероятностью может произойти рекомбинация РНК этих вирусов, из-за чего возникнет новый вирус, обладающий способностью передаваться от человека к человеку (как обычный), но с высокой смертоносностью (как «птичий»). Просчитывать опасность и вероятность такого события я не возьмусь, так как я вообще не специалист в этой области (эх, было бы здорово, если бы такую фразу говорили все неквалифицированные теоретики). Но я призываю увидеть следующую возможность пользы от «свиной паники»: люди постараются меньше подставляться (реже ходить в общественные места, чаще мыть руки, проветривать помещения), что уменьшит активность «обычного» гриппа в этом году. А это уже снижает вероятность рекомбинации РНК двух разных вирусов в ближайшее время, что похоже на реальную пользу.

Хорошей вам недели! И крепкого здоровья!

Нам не дано предугадать

Что отнято судьбой, а что подарено, -
В конце концов не все ли мне равно?
(c) Михаил Щербаков
(впрочем, по совсем другому поводу)

Иногда ощущение чрезвычайной важности текущего момента просто зашкаливает - кажется, что именно в данную секунду решается судьба. Оглянувшись назад через несколько лет, мы понимаем, что так и было - одно давнее случайное решение сделало жизнь именно такой, какая она есть.

Год назад мы уже поднимали тему сомнений человека, которому предстоит определить чужую судьбу (всего лишь какой-то её элемент). А в воскресенье мне попался выпуск передачи «Личные вещи», в которую был приглашён Дмитрий Певцов.

Его актёрская судьба началась очень странно - со вступительных экзаменов в педагогический ВУЗ. Как Дмитрий сказал, его выгнали с экзамена по химии, потому что поймали со шпаргалкой. Возможно, кто-то тогда переживал: «Как же так? Лишили ребёнка возможности стать учителем! Пожалели бы чуть-чуть!»

Но его выгнали с экзамена, не взяли в ВУЗ, поэтому Дмитрий не стал учителем. А стал слесарем. Частые гости «Ленкома», возможно, удивятся, как можно такого Фигаро ставить за слесарный станок :)

Но оказалось, что работа на заводе дала будущему актёру две важных вещи:
1. Он понял, что категорически не хочет стоять всю жизнь за станком.
2. Имея 7 часов рабочего времени, в течение которых голова не занята совсем, Дмитрий мог о многом думать.

И второй пункт мощным рывком притянул его к книгам и театру. Как он сказал, «начал ходить в театр сам, а не с родителями». Ну а после этого всё было как у всех :) А представьте, что ему попались бы не такие строгие экзаменаторы!

Почти всегда мы не имеем достаточных знаний о будущих следствиях своих решений (если бы имели, то и решать бы не пришлось - сразу знали бы, какой вариант лучше). Кого-то всю жизнь поддерживают, но он ничего не достиг. А кому-то постоянно вставляют палки в колёса, но он выше всех.

Мы не знаем будущего, поэтому пора перестать кипятить собственный мозг в подобных случаях. Колебаться и напрягаться надо только в тех ситуациях, когда о раскладе имеется хоть какая-то информация. Не надо себя накручивать, потому что мы не можем всего предусмотреть. Делайте так, как кажется правильным!

Хорошей вам недели!

Как поломаться в волейболе?

Миллионы людей годами игают в волейбол и другие интересные виды спорта, получая массу удовольствия, но ни разу не увидев травм. Но надо понимать, что порой это не заслуга человека и его команды, а просто везение. Чтобы меньше полагаться на удачу, я постарался перечислить некоторые типы ошибок. Год назад опубликована заметка Ода волейболу, а сейчас пришло время дополнить её перечнем распространённых способов испортить себе вечернюю тренировку.

Удобно разделять ошибки на командные-дисциплинарные и индивидуальные-технические. Говоря «дисциплина», мы подразумеваем слаженные командные действия. Многие ситуации отрабатываются на тренировках, чтобы закрепить у команды навык правильно и без суеты с ними справляться. Соответственно, желание выиграть очко на индивидуальном мастерстве можно поощрять только в том случае, если это не противоречит заранее оговоренным действиям всей команды. Если же противоречие возникает, то растут риски для здоровья игроков, что нельзя допускать ни в профессиональном, ни в любительском спорте. Поэтому чрезмерное рвение «всё сделать самому» надо пресекать, если не хочется лишний раз ездить в травмпункт.

Примеры травм из-за плохой дисциплины:

- Соперник не справился с приёмом, поэтому мяч переходит на нашу сторону. В этот момент разыгрывающий решает сразу отдать пас, потому что траектория мяча достаточна удачна (как раз опускается во вторую зону). И в этот же момент нападающий решает ударить по этому удобному мячу. Естественно, нападающий снимает мяч выше разыгрывающего и зарабатывает очко. Но он приземляется на разыгрывающего, который никак не ожидал получить со всего размаху локтем по носу. Все живы, но пострадали оба. Я видел подобный расклад несколько раз, поэтому считаю, что его стоит много раз представить в голове, чтобы выработать свои правильные действия на такой случай.

- Доводка подачи чуть-чуть за трос вынуждает не очень высокого разыгрывающего отдавать аварийную передачу низкого качества, поэтому нападающие из пятой и четвёртой зон не понимают, кому из них следует атаковать. Результат: на мяч идут оба. Разогнавшийся игрок второй линии уже не может остановиться (потому что не касается земли), а затянувшийся нападающий из четвёрки сначала бьёт его по лицу (на замахе), а уже потом играет в мяч. По счастливой случайности, глаза не пострадали, но кровью площадку залили, так как основательно рассекли бровь.

- Блокирующий хорошо поднимается с вражеским нападающим, поэтому тот решает увеличить шансы на позитивный для себя исход - вместо удара выполняет скидку за блок. Либеро видит этот манёвр и прыгает на спасение падающего мяча. Но блокирующий не чувствует этого действия, поэтому пытается подцепить падающий мяч, не глядя на него - и своей тяжёлой «клешнёй» цепляет голову страхующего. Опять же, глаза целы, но нагрузка на шею была большая, поэтому либеро из игры выбыл.

Все эти случаи могли пройти гораздо мягче, если бы игроки сработали дисциплинированнее. В сомнительных случаях более решительный игрок должен громко сообщить голосом, что он идёт на мяч - тогда остальные как минимум не будут ему мешать. Это позволит увереннее действовать, что увеличит эффективность игроков, но это не самое главное. Главное - это уменьшит количество и серьёзность травм. Сообщайте о своих неочевидных намерениях голосом и не трогайте чужой мяч.

К списку распространённых индивидуальных ошибкок я бы отнёс следующий технический брак:

- Травмы пальцев на блоке (из-за неправильной постановки блока или очень контактной игры на сетке) - надо жёстко судить касания сетки и выполнять только осмысленный (т.е. правильный) блок.

- Травмы голеностопа при приземлении на кого-то. Следует жёстко судить заступы, чтобы уменьшать вероятность таких травм. Если собрались команды с игроками очень разных уровней, то лучше не блокировать неумелых нападающих - они могут влететь в сетку, покалечив и себя, и блокирующих. Лучше сначала присмотреться к их манере атаковать, чтобы быть увереннее в малых шансах на подобные глупости.

- Удары локтями по голове или шее после постановки группового блока. Эта ошибка часто проявляется у начинающих игроков, которые не умеют аккуратно убрать свои руки после двойного или тройного блока, поэтому широкими резкими движениями калечат игроков своей же команды. Данный элемент надо многократно отрабатывать на тренировках. И не стоит пристраиваться на групповой блок к незнакомым людям в новой компании - запросто можно лишиться прямоты носа.

Это было расширение перечня из прошлогодней заметки Волейбол - безопасная игра. Надеюсь, кому-то данное перечисление ошибок позволит больше радоваться и меньше ходить в гипсе и пластыре :)

Волейбол - это очень интересная и здоровая игра. Но если делать глупости, то и воздушным шариком можно покалечиться. Поэтому постоянно надо оценивать риски и работать над своей техникой и командной дисциплиной. Берегите себя!

Слова имеют значение

Идея что-нибудь сделать для изменения своего веса, наверное, приходила в головы женщин во все времена. В какие-то периоды этим меньше заморачивались, в какие-то - больше. Присказка «ничего не ем, а толстею» знакома человечеству очень давно.

Недавно я услышал следующий рассказ от человека, прошедшего вторую мировую войну: «До войны тоже все хотели худеть, тоже говорили, что ничего не едят, а вес откуда-то сам появляется. А потом начались настоящие голодные годы: еды было очень мало, а работать для победы надо было обязательно. И все стали стройными как лани».

Это всего лишь пример неправильного употребления фразы «ничего не ем». Слова имеют значение, поэтому важно их корректно использовать.

В прошлой заметке мы говорили о ненормативной лексике в интернете. В опросе приняло участие почти 500 человек, результаты вышли вполне ожидаемыми:

- 3% отметили, что им нравится читать и слушать ненормативную лексику,

- 2/3 проголосовавших предпочитают грамотный текст без мата,

- чуть больше половины проголосовавших не смущаются, увидев матерное выражение в тексте, потому что им важнее смысл, а не форма. Другими словами, они не испытывают восторга от ненормативной лексики, если в тексте есть смысл (иначе бы проголосовали за первый пункт),

- больше четверти согласились, что иногда невозможно поделиться ссылкой на интересный материал с родственниками и подругами, потому что тем будет неприятно читать некоторые слова.

Отмечу, что результаты этого голосования, скорее всего, заметно отличались бы от выводов аналогичного опроса на других блогах - многое зависит от специфики аудитории. Но главная цель достигнута - мы убедились, что есть читатели, которые признают текст интересным для себя, но не могут делиться им с близкими людьми.

Для блоггеров это означает следующее:

- надо употреблять ненормативную лексику, если хочется внимания 3% аудитории этого блога,

- если же избегать неосмысленного использования ненормативной лексики, то можно получить внимание 28% аудитории этого блога + их родственников и друзей.

Слова имеют значение, поэтому их надо правильно использовать.

Хорошего вам окончания недели!

mama.yandex.ru

Бывают люди, которым неприятно слышать и читать мат. Нет, они давно знают все эти слова, разного уже наслушались за свою жизнь, в обморок от произнесённой кем-то тирады не падают. Но им неприятно. Это их особенность. Распространённый пример - старшие родственники.

Я не матерюсь в блоге, потому что не испытываю такого желания. И знаете, это очень приятно, когда родные люди читают блог, когда они звонят по телефону или устно делятся своими мыслями о какой-то заметке («оставлять комментарии слишком сложно для нас»). И им нравится, что здесь они «могут спокойно и комфортно читать, не ожидая баннера с голыми туловищами на весь экран или откровенных выражений на тему процесса размножения».

Когда меня спрашивают родственники, какие ещё есть блоги, то я не могу порекомендовать им взглянуть на рейтинг блогов Яндекса. Из первой тридцатки лично я знаю далеко не всех, но сходу вспомнил пятерых, которые пишут иногда интересно, но своей манерой изложения особенно огорчат женскую половину представителей старшего поколения. Есть даже блоги, названия которых содержат ту самую лексику, с которой многим людям очень неприятно без надобности сталкиваться.

Короче, к делу. Пожалуйста, оставьте своё мнение о предпочтениях в этой области (в голосовании можно выбирать несколько вариантов ответов). Хотелось бы понять, только ли я часто не могу позволить себе поделиться с родственниками интересной ссылкой из-за того, что их расстроит неприемлемая лексика. Или может кто-то ещё ловил себя на таких мыслях?

Я вовсе не призываю как-то ограничивать авторов, пусть пишут что хотят. Лично мне легко читать «даже топовых блоггеров». Но если бы был сервис для желающих, сужающий интернет до такого, который «маме нравится», то мне было бы гораздо проще рекомендовать родным поискать что-то в сети самим. Грубо говоря, сейчас для моей мамы интернет - это система, с которой нельзя расслабиться: в любой момент можно столкнуться с ругающимися малолетками, неожиданно может выскочить баннер с порнухой, который невозможно закрыть, повсюду вирусы и так далее. А хотелось бы понизить вероятность таких факторов на пару порядков.

Кстати, поисковые системы последние годы взялись за борьбу с некоторыми типами проблем - в результатах поиска иногда можно встретить предупреждение о вредоносности сайта. Но хотелось бы увидеть специальный «яндекс для родителей», чтобы они реже морщились, изучая мировую паутину. Согласитесь, простейшее регулярное выражение позволит с очень высокой надёжностью рассортировать, например, блоги, что позволит выделить «родительское» подмножество из имеющегося каталога блогов.

А какое у вас и ваших родственников отношение к ненормативной лексике? Возникает ли иногда желание отгородиться самим или хотя бы их закрыть от мата?

Завершая заметку, хочу порекомендовать блог, который уверенно вошёл бы в «каталог для родителей», потому что он специально создан для молодых родителей. Заметки блога orangefrog посвящены творческому подходу к обучению и воспитанию, разбору сложных взаимодействий родителя с ребенком и так далее. На мой взгляд, из многих сайтов о детях данный выделяется высокой концентрированностью - заметки состоят из коротких и ёмких пунктов, которые почти всегда интересно прочитать.

Хорошей вам недели!

Внимание, в комментариях к этой заметке присутствует ненормативная лексика.

Интенсивность воздействия

Человеку свойственно получать удовольствие от самого процесса творчества. Но из-за странного своего устройства он никогда не может насытиться. Поэтому почти каждый творец старается выплёскивать результат своей деятельности максимально ярко.

Но что может сделать начинающий музыкант? Он может добавить громкости! И именно это мы почти всегда видим на любительских концертах: усилитель выводится на максимальную громкость, но хрипы из динамиков мало смущают молодых исполнителей. Такое ощущение, что они уже убили свои уши, а теперь калечат зрителей. Хорошо, что иногда на сцену выходят молодые музыканты, отличающие интересную музыку от закладывающей уши.

Что может сделать увлекающийся кино человек с видеокамерой? Снимать длиннющие и предельно занудные ролики, содержащие массу необоснованных повторов! И именно это мы видим почти всегда на фестивалях любительского кино: часто плотность идей крайне низка, поэтому силы на следующее посещение подобного мероприятия приходится долго копить. Хорошо, что иногда попадаются талантливые видеоролики - ради них всё.

Что может сделать писатель/блоггер, чтобы усилить своё воздействие? Писать часто и много! Именно так он увеличивает вероятность контакта с аудиторией. И именно так он понижает качество этого контакта. Нормой стало «чтение по диагонали», потому что уж очень большие объёмы текста приходят каждый день в rss-reader, так ведь?

Очень трудно найти в себе силы, чтобы стереть половину абзаца, а остаток переработать, потому что жалко уже вложенные силы. Некоторые заметки мне удавалось сократить в два-три раза, но это не столько работа с текстом, сколько борьба с собой: «Смысл выразил, который хотел? Раз так, то не надо дальше ужимать!» Надо! И я понимаю молодых авторов короткометражного кино - им трудно смириться с тем, что вполне годный видеоматериал не будет показан большой аудитории. Но и им тоже надо понять, что короткое и ясное изложение идеи притягивает, давая шансы на дальнейшее общение со зрителем, а невнятность и бездарная трата времени отдаляют.

Это 250-ая заметка блога, хотя ему ещё и двух лет нет. Я не хочу пустого кокетства на тему «слишком часто я пишу, надо больше думать», поэтому завершу эту заметку ссылкой на старую запись с историей о том, как можно почувствовать важность высокой плотности содержания. Если судьба заставляет почему-то жить в узких рамках, то человек вынужден оптимизировать свои действия не самым очевидным способом. Но зачем дожидаться такого подарка пинка судьбы?

Можно начать действовать интенсивно уже сейчас. Не громче и дольше, а качественнее и плотнее. Хорошей вам недели!

Треугольник и бесконечность

Если использование некоторого инструмента всегда приводило к успеху, то это ещё не доказывает, что данный инструмент абсолютно надёжен. Даже если человек придумал набор правил, по которым торгует на фондовом рынке уже 5 лет, имея ежегодный доход, например, 150-350%, то это не гарантирует ему успеха в следующие годы.

Но если всё поломать, используя инструмент неправильным образом, то винить во всём его - более, чем странное дело. Если специалист рассказал, какие именно действия следует предпринимать, а слушатель решил часть из них делать «чуть-чуть иначе», а часть не делать вообще, то глупо потом ругаться со специалистом об его «дурацкой неработающей методике». Потому что в такой ситуации виноват не инструмент, а его пользователь.

Мне часто приходится сталкиваться с неправильным использованием математики. Неспециалист начинает применять сложные техники (о которых что-то где-то слышал) неправильным способом, а потом удивляется очевидно некорректным результатам. При этом он не готов понять, что его вольное обращение с тонким понятием приводит ко всем проблемам, а винит во всем математиков, которые занимаются ерундой и ничего не понимают. Ну а чтобы доказать, что его подход к пониманию вопроса является корректным, неспециалист с его помощью доказывает какое-нибудь верное утверждение (и даже не понимает глупости происходящего - из ложного можно доказать как ложное, так и истинное, а из верного только верное).

Одна из любимых тем многих спорщиков - бесконечность. Это сложное понятие, использовать которое следует очень аккуратно, если хочется оставаться в рамках математики, а не уходить в некорректные бредни. Многие математики долго думали, как надо ограничить обращение с этим понятием, чтобы разговоры о бесконечности вообще имели смысл (помогали доказать что-то верное, но не позволяли порождать ложь). Впрочем, чтобы осознать всё это, спорщикам требуется освоить как минимум логику, чтобы отличать верные утверждения от ложных. Но зачем это делать, если можно работать с понятием бесконечность «как интуиция подскажет»?

Продолжим примером задачки о прямоугольном треугольнике, который не сдаётся. Сегодня мы «докажем», что длина любой стороны треугольника равна сумме длин двух других сторон. Для простоты будем работать с прямоугольным треугольником (это нам попутно позволит опровергнуть теорему Пифагора).

Итак, разделим два катета прямоугольного треугольника пополам. Те половинки, что выходят из прямого угла, сдвинем в сторону гипотенузы (как на картинке справа). При этом ни одного кусочка катетов мы не потеряли, поэтому их суммарная длина не поменялась.

Теперь разрежем пополам четыре образовавшихся кусочка исходных катетов. Выберем из появившихся четвертинок те, которые соседствуют с прямыми углами. И их тоже сдвинем в сторону гипотенузы.

Так можно продолжать бесконечно: катеты будут приближаться всё сильнее и сильнее к гипотенузе, но их суммарная длина не поменяется, потому что все элементы просто двигаются по плоскости. В пределе мы получим полное совпадение гипотенузы и зигзагообразной ломаной, получившейся из двух сторон треугольника, потому что отклонение ломаной от гипотенузы будет стремиться к нулю. А суммарная длина катетов будет стремиться к длине гипотенузы, становясь сколь угодно близкой к ней. Другими словами, в любом прямоугольном треугольнике длина гипотенузы равна сумме длин катетов.

Это очень полезный результат, потому что он делает многие геометрические задачи очень простыми, разгружая голову школьников для более полезных дел. Полагаю, скоро в комментариях появятся подробные объяснения, почему так делать нельзя :)

Хорошей вам недели!