Если использование некоторого инструмента всегда приводило к успеху, то это ещё не доказывает, что данный инструмент абсолютно надёжен. Даже если человек придумал набор правил, по которым торгует на фондовом рынке уже 5 лет, имея ежегодный доход, например, 150-350%, то это не гарантирует ему успеха в следующие годы.
Но если всё поломать, используя инструмент неправильным образом, то винить во всём его - более, чем странное дело. Если специалист рассказал, какие именно действия следует предпринимать, а слушатель решил часть из них делать «чуть-чуть иначе», а часть не делать вообще, то глупо потом ругаться со специалистом об его «дурацкой неработающей методике». Потому что в такой ситуации виноват не инструмент, а его пользователь.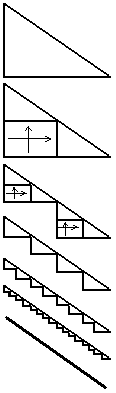
Мне часто приходится сталкиваться с неправильным использованием математики. Неспециалист начинает применять сложные техники (о которых что-то где-то слышал) неправильным способом, а потом удивляется очевидно некорректным результатам. При этом он не готов понять, что его вольное обращение с тонким понятием приводит ко всем проблемам, а винит во всем математиков, которые занимаются ерундой и ничего не понимают. Ну а чтобы доказать, что его подход к пониманию вопроса является корректным, неспециалист с его помощью доказывает какое-нибудь верное утверждение (и даже не понимает глупости происходящего - из ложного можно доказать как ложное, так и истинное, а из верного только верное).
Одна из любимых тем многих спорщиков - бесконечность. Это сложное понятие, использовать которое следует очень аккуратно, если хочется оставаться в рамках математики, а не уходить в некорректные бредни. Многие математики долго думали, как надо ограничить обращение с этим понятием, чтобы разговоры о бесконечности вообще имели смысл (помогали доказать что-то верное, но не позволяли порождать ложь). Впрочем, чтобы осознать всё это, спорщикам требуется освоить как минимум логику, чтобы отличать верные утверждения от ложных. Но зачем это делать, если можно работать с понятием бесконечность «как интуиция подскажет»?
Продолжим примером задачки о прямоугольном треугольнике, который не сдаётся. Сегодня мы «докажем», что длина любой стороны треугольника равна сумме длин двух других сторон. Для простоты будем работать с прямоугольным треугольником (это нам попутно позволит опровергнуть теорему Пифагора).
Итак, разделим два катета прямоугольного треугольника пополам. Те половинки, что выходят из прямого угла, сдвинем в сторону гипотенузы (как на картинке справа). При этом ни одного кусочка катетов мы не потеряли, поэтому их суммарная длина не поменялась.
Теперь разрежем пополам четыре образовавшихся кусочка исходных катетов. Выберем из появившихся четвертинок те, которые соседствуют с прямыми углами. И их тоже сдвинем в сторону гипотенузы.
Так можно продолжать бесконечно: катеты будут приближаться всё сильнее и сильнее к гипотенузе, но их суммарная длина не поменяется, потому что все элементы просто двигаются по плоскости. В пределе мы получим полное совпадение гипотенузы и зигзагообразной ломаной, получившейся из двух сторон треугольника, потому что отклонение ломаной от гипотенузы будет стремиться к нулю. А суммарная длина катетов будет стремиться к длине гипотенузы, становясь сколь угодно близкой к ней. Другими словами, в любом прямоугольном треугольнике длина гипотенузы равна сумме длин катетов.
Это очень полезный результат, потому что он делает многие геометрические задачи очень простыми, разгружая голову школьников для более полезных дел. Полагаю, скоро в комментариях появятся подробные объяснения, почему так делать нельзя :)
Хорошей вам недели!
19 окт. 2009 г.
Треугольник и бесконечность
Темы:
математика,
образование
Подписаться на:
Комментарии к сообщению (Atom)
Понравилась заметка? Подпишитесь на
RSS-feed или email-рассылку.
Хотите поделиться ссылкой с другими? Добавьте в закладки:
Есть вопросы или предложения? Пишите письма на адрес mytribune АТ yandex.ru.
С уважением,
Илья Весенний
RSS-feed или email-рассылку.Хотите поделиться ссылкой с другими? Добавьте в закладки:
Есть вопросы или предложения? Пишите письма на адрес mytribune АТ yandex.ru.
С уважением,
Илья Весенний
„ни одного кусочка катетов мы не потеряли, поэтому их суммарная длина не поменялась“
ОтветитьУдалить„суммарная длина катетов будет стремиться к длине гипотенузы“
Второе утверждение ложное. Ваше докозательство основано на лжи.
да, забыл сказать, математика не физика, тут нету понятия „элементарной неделимой длины“ на подобие „элементарной частицы“. Катеты никуда неисчезнут, сколько не дроби...
ОтветитьУдалитьНу кстати подобный финт можно провернуть с любым треугольником. не обязательно с прямоугольным.
ОтветитьУдалитьПочему же нельзя, так делать можно, только результата этого не получить.
ОтветитьУдалитьИз того, что отклонение гипотенузы стремится к нулю при стремлении количества треугольников к бесконечности, ещё не следует, что суммарная длина всех катетов стремится к гипотенузе. Когда речь идёт о бесконечных величинах (бесконечно больших или бесконечно малых), важно не только то, ЧТО величина стремится к бесконечности, но и то, КАК она стремится.
В данном случае, при стремлении числа отрезков к бесконечности, длины всех рассматриваемых отрезков отрезков не меняются вообще.
Для любого n, СУММ i=1,n (a/n) = a
Или так:
ОтветитьУдалитьесли a + b ≠ c то
для любого n, n*(a/n) + n*(b/n) ≠ n*(c/n)
Если бы Вы предложили построение, которое привело бы к такой конструкции:
ОтветитьУдалить∑i=1,n (Ai+Bi) = ∑i=1,n Ci + o(Ci),
то, при n→∞, Вы удивили бы Евклида..-)
А проблема не опять ли в чертеже, случайно? Такое ощущение, что точка пересечения этих серединных перпендикуляров не будет лежать на гипотенузе.
ОтветитьУдалитьДля математики доказанное - бред.
ОтветитьУдалитьНо в жизни именно так и считают.
Иначе как определить длину береговой линии. Берут некий масштаб и сглаживают все гипотенузами!
Нет, denlion, не в чертеже - тут всё честно. Илья честный обманщик - он обманывает только в одном месте "доказательства". Это место указано в третьем абзаце первого комментария.
ОтветитьУдалитьУважаемый аноним, а где мы пользуемся элементарной неделимой длиной? Где мы говорим, что катеты куда-то исчезают?
ОтветитьУдалитьВ рассуждении выше речь идёт о том, что катеты просто постепенно перекладываются, сохраняя свою длину, но становясь сколь угодно похожими на гипотенузу.
creat0r, в заметке я писал, что мы работаем с прямоугольным треугольником исключительно для простоты (и поддержания традиции :)
Данное рассуждение применимо к любому треугольнику, что очень упростило бы всю геометрию.
abyrvalg, а разве кто-то спорит с тем, что «Для любого n, СУММ i=1,n (a/n) = a»? Я как раз пользуюсь тем, что от того, что мы измельчили катеты, сделав из них ломаную, их длина не поменялась. А раз ломанная будет сколь угодно близка к гипотенузе в пределе, то и её длина будет сколь угодно близка к длине гипотенузы. Значит, сумма длин катетов равна длине гипотенузы. В чём ошибка? ;)
denlion, чертёж не идеальный, но дело не в нём.
кстати, так можно доказать, что периметр круга и квадрата равны, если диаметр и длина стороны квадрата равны.
ОтветитьУдалитьСуммарна длина катетов не меняется, следовательно, и не стремится :)
ОтветитьУдалитьБесконечно малый треугольник - это все-равно треугольник, и простым суммированием здесь не отделаешься.
ОтветитьУдалитьНасколько я помню, там выползают "пределы" и все расставляют по местам.
Площадь между ломаной и гипотенузой действительно стремится к нулю как ab/2n, где n-количество треугольников. Но длина ломаной никак не стремится к длине гипотенузы, а стремится к a + b.
ОтветитьУдалитьНеправомерен переход "ломаная бесконечно близко приближается к прямой, поэтому их длины совпадут". Приближение мы смотрим на плоскости (они совпадают по занимаемой площади и по форме), а выводы делаем относительно совсем другого одномерного параметра - длины.
ОтветитьУдалитьpavel, верно, так вообще много интересного можно доказать :)
ОтветитьУдалитьabyrvalg, я не совсем понимаю Вашу фразу «Но длина ломаной никак не стремится к длине гипотенузы, а стремится к a + b». Длина ломаной равна a+b, а не стремится к этому значению (потому что мы не теряли кусочки ломаной, когда её строили). И длина ломаной равна длине гипотенузы, потому что ломаная стремится к гипотенузе. Поэтому a+b=c (где c - длина гипотенузы).
в любом же случае останется бесконечно малый, но таки прямоугольный треугольни. у которого есть гипотенуза никак не равная катетам.
ОтветитьУдалитьTyr, в нашей, сложившейся системе объектов и понятий быть такого, безусловно, не может.
ОтветитьУдалитьНо тут речь идёт о том, чтобы точно и однозначно указать ошибку в рассуждениях Ильи. (Гляжу на себя в зеркало - вижу собаку: глаза умные. но молчит!)
Итак:
1. Чертёж верен (это на всяк случ..-)
2. Длина ломаной верна.
3. Есть ломаная и прямая. Площадь фигуры, ими образованной, стремится к нулю.
4. При этом, ломаная в прямую не переходит при стремлении n в ∞.
Осталось обосновать 4.
Пусть n - число треугольников, на которые мы разбиваем исходный треугольник. Тогда величины "длина гипотенузы" и "сумма длин катетов" будут стремиться к нулю при n стремящемся к бесконечности. Сумма длин сторон треугольника не может равняться нулю, т.к. в этом случае треугольник превращается в точку. Следовательно, утверждение о равенстве этих двух величин неверно.
ОтветитьУдалитьНа самом деле непонятно, почему из стремления ломаной из катетов к гипотенузе следует вывод о равенстве их длин? Честно, просто связи не вижу. Кстати, в доказательстве надо расшифровать фразу "ломаная стремится к гипотенузе".
ОтветитьУдалитьЕсли придерживаться точки зрения, что все сделанные поступки изменяют карму, то у читающего этот топик сейчас 2 пути:
ОтветитьУдалить1. Признать, что при стремлении разницы между точками к нулю при стремлении некоторого параметра к бесконечности, эти точки в пределе сливаются в одну и ту же фигуру независимо от того, как они стремятся. После этого забыть Пифагора и жить с этим дальше.
2. Аргументированно возразить, что, как ни уменьшай треугольник, в прямую он не перейдёт, несмотря на то, что разница между точками гипотенузы и катетов стремится к нулю с ростом количества треугольников.
Чтобы показать 2. надо бы понимать критерий стремления одной фигуры к другой. Здесь, фактически, предлагается критерий: если точки одной фигуры стремятся к точкам другой фигуры, то в пределе эти фигуры совпадают.
У совпадающих фигур все параметры, понятно, равны.
Мне не нравится в таких заданиях то, что чтобы найти ошибку в таком "доказательстве" нужно сначала согласиться, что это именно ДОКАЗАТЕЛЬСТВО :)), чего здесь просто нет! Я могу по индукции легко доказать, что сумарная длина катетов всех таких новообразованных катетов не изменится, например, первый шаг индукции вы показали сами в первой картинке, т.е. все логично.
ОтветитьУдалитьА вот с какой стати при стремлении к бесконечности сумма длин катетов должна совпасть с гипотинузой я даже понять не могу, поэтому не могу понять смысл такой задачи :))
Да при стремлении к бесконечности катеты новых треугольников будут делиться пополам с каждым шагом, но и КОЛ-ВО таких катетов будет удваиваться...
В общем, не понимаю я этого доказательства :)
trasher, логика следующая:
ОтветитьУдалить1. все точки ломаной стремятся к точкам гипотенузы при n→∞ (выбираем произвольно малое число ε, для него всегда найдётся n такое, что все точки ломаной ближе ε к гипотенузе).
2. если все точки одной кривой стремятся ко всем точкам другой кривой, то они совпадают при n→∞.
3. если две кривые совпадают, то и все из характеристики совпадают.
Илья, мне кажется необоснованным п.2.
Илья, есть подозрение, что причина того, что ломаная не стремится к гипотенузе может быть обоснована тем, что производная гипотенузы гладкая (более того - константа), а производная ломаной разрывная, причём количество разрывов растёт с числом n, и в пределе бесконечно.
ОтветитьУдалитьНа этом пока мысль останавливается.
Andrew, длина гипотенузы и сумма длин катетов не меняются из-за каких-то разрезаний, так как мы не теряем ни одного кусочка.
ОтветитьУдалитьtrasher, конечно, приведённое выше - не доказательство! Я даже специально в заметке слово «доказательство» брал в кавычки.
А смысл этого упражнения вот в чём: если человек считает приведённое некорректное рассуждение доказательством, то его легко обмануть. Соответственно, разбор подобных задачек тренирует критичность головы: чтобы меньше обманывать самого себя и реже позволять кому-то обманывать себя.
дак эцсамое
ОтветитьУдалить"Длина ломаной равна a+b, а не стремится к этому значению (потому что мы не теряли кусочки ломаной, когда её строили). И длина ломаной равна длине гипотенузы, потому что ломаная стремится к гипотенузе."
Вот же вранье :)
Либо уж она (длина ломаной) равна фиксированному значению, то есть a+b, либо она куда-то там стремится
Паша, почему же? Длина ломаной равна фиксированному значению a+b. И она же равна длине гипотенузы c. Это ничему не противоречит. И уж конечно длина никуда не стремится, потому что является числом.
ОтветитьУдалитьПоэтому a+b=c. Всё чисто! :)
Рассмотрим наш треугольник. Пусть гипотенуза - c, а один из острых углов - α. В таком случае, если принять сумму длин катетов равной гипотенузе, мы получим c*cosα + c*sinα = c -> sinα + cosα = 1 -> 1 + sin2α = 1 -> sin2α = 0 -> α = 0, чего быть не может.
ОтветитьУдалитьAndrew, Ваша позиция понятна: Вы показали, что «доказанное» утверждение о равенстве сумм длин катетов и длины гипотенузы не может быть верным. Но это не требовалось, потому что все и так прекрасно это знают.
ОтветитьУдалитьПредставьте, что аналогичным способом кто-то «доказал» верное утверждение. Тогда Ваше рассуждение для опровержения доказательства было бы нельзя применить, так как оно работает только для ложных утверждений. Но уметь опровергнуть такое «доказательство» очень полезно, потому что способность отличать корректное от некорректного очень важна при поиске истины.
Судя по комментариям, не все поняли "доказательство". Длина ломаной постоянна (равна a+b) при любом числе n ее колен. Длина отрезка прямой тоже постоянна (равна с), ведь с ним ничего не происходит. При n стремящимся к бесконечности, точки ломаной стремятся к точкам отрезка, так как расстояние от них до отрезка стремиться к нулю. Все это верно. Далее следует вывод, что при n стремящимся к бесконечности ломаная совпадет с отрезком (превратится в отрезок). Следовательно, совпадут длины ломаной и отрезка: a+b=c.
ОтветитьУдалитьВидимо ошибка в выводе о совпадении форм ломаной и отрезка при n стремящимся к бесконечности. Чтобы их формы совпали недостаточно только увеличения числа колен ломаной. Наверное надо, чтобы ломаная постепенно распрямлялась.
Вы затронули важную проблему. Здесь могут запутаться даже математики. Но они вскоре найдут свои ошибки. Хуже обстоит дело с техническими науками. Там подобные ошибки лежат в фундаменте теорий. И никто их не находит. И попробуй что-то изменить через 40 лет, когда все обросло кучей монографий уважаемых ученых. Посмотрите, например, на комментарий polnedoma@gmail.com.
Я тут подумал, а ведь всё же правильно. И доказательство верное. Просто нужно переопределить понятие треугольника =) И, между прочим, на рисунках этот треугольник никак не будет отличаться от "настоящего". Ну, подумаешь, теоремы немного поменяются.
ОтветитьУдалитьСергей, умозрительно понятно, что поточечного стремления недостаточно. Но насколько гладкой должна быть предельная "ломаная"? Достаточно ли непрерывности первой производной? Вроде бы да, но надо доказать.
ОтветитьУдалитьК тому же, есть подозрение, что развенчать "доказательство" Ильи надо без применения понятий функциональных последовательностей и прочих "критериев Коши". По крайней мере, треугольники высшей математики раньше не требовали.._)
Парадокс основан на том заблуждении, что если каждый элемент последовательности обладает некоторым свойством, то этим свойством должен обладать и предел последовательности. Аналогичным образом можно "доказать", например, что число пи рационально (как предел последовательности рациональных чисел 3, 3.1, 3.14, 3.141, ...), экспонента - это многочлен, а размерность любого фрактала на плоскости равна двум.
ОтветитьУдалитьЕсли уж применять другие методы математики, то лучше теорию фракталов. Если мне память не изменяет, то еще Мандельброт еще занимался этим вопросом(стояла задача определить длину побережья, а при увеличении масштаба в 10 раз длина побережья увеличивалась, вроде, в 1,3 раза.) Так что впринципе прямая бесконечной длины, такая как замкнутая кривая Коха(крест, треугольник) может образовывать фигуру конечной площади. Ошибка в том что Илья заявляет что будто бы ступенчатая кривая сольется с гипотенузой, такого не произойдет. Треугольники никогда не обратятся в точку, они всегда будут треугольниками, несмотря на то что это притиворечит физическому миру.
ОтветитьУдалитьА по поводу технических наук вспоминается пример про формулу частоты колебаний маятника, на первом курсе мы ее выводили на лекции по физике и оказалось что при выводе используется приближение sin(a)=a и формула верна для малых углов, и нам преподаватель на этом примере показал что при дальнейшем ее использовании нужно помнить чем мы пренебрегали при выводе и не использовать бездумно, что бы не попасть в конфуз в нестандартных применениях.
Можно заметить, что построенная кривая сходится только по мере к гипотенузе, а почти всюду она кстати (или не кстати) не сходится.
ОтветитьУдалитьЗдравствуйте, Илья. Во-первых, спасибо вам за интересный блог, с некоторых пор с удовольствием вас читаю.
ОтветитьУдалитьПо поводу "доказательства" — ошибка как минимум вот в этом переходе:
А суммарная длина катетов будет стремиться к длине гипотенузы, становясь сколь угодно близкой к ней. => Другими словами, в любом прямоугольном треугольнике длина гипотенузы равна сумме длин катетов.
Даже если мы каким-то образом доказали, что lim[n→∞] CУММЫ(i=1,n, ai+bi) равен длине изначальной гипотенузы, то из этого нельзя сделать более общий вывод о том, что то же самое будет верно при конечном n.
Можно еще уточнить мое объяснение некорректности доказательства при помощи метода мат. индукции.
ОтветитьУдалитьБаза индукции: при n→∞ ∑(i=1,n, ai+bi) = С
Переход: для любого k также верно: n→k-1 ∑(i=1,n, ai+bi) = С.
Переход очень просто доказать: ∞-1 = ∞
Я думаю, у людей, неверно оперирующих понятием бесконечности, в голове интуитивно происходит примерно то же самое :)
Однако это доказательство нельзя применять для конечных k, т.к. сколько не отнимай от бесконечности единицу, останется бесконечность.
Если же предположить, что мы отнимаем единицу бесконечное количество раз, получим неопределенность.
Следовательно, совершить переход от бесконечных k к конечным невозможно.
Сергей, спасибо за более подробное изложение "доказательства". Разделяю Ваши опасения про массу некорректных выводов, сделанных без понимания сути.
ОтветитьУдалитьabyrvalg, по поводу Ваших слов «треугольники высшей математики раньше не требовали» могу только уточнить, что мы в приведённом "доказательстве" используем очень сложное понятие бесконечности. И именно в этом состоит проблема: мы неправильно его используем, поэтому получаем очевидную ерунду. Можно было получить доказательство менее очевидной теоремы, неправильно работая с бесконечными величинами... Важно понимать свойства используемых объектов, чтобы не допускать таких ошибок.
Уважаемый аноним, спасибо за прекрасный пример с числом Пи!
al31f, благодарю за пример с маятником! Он тоже очень подходит для объяснения "парадокса".
Shedal, спасибо за тёплые слова!
Сейчас сильно не думается, из-за простуды, но есть 2 версии:
ОтветитьУдалить1. Бывают разные бесконечности. Насколько я помню - как мощности у множеств (например, натуральных чисел бесконечно, и иррациональных чисел бесконечно много, но при этом иррациональных "больше"). Вполне возможно, что и здесь стремление к бесконечности по количеству разбиений одно, а по фигуре, полученной в результате разбиения - другое...
2. Тут уже вспоминали про епсилон-окресности с точки зрения стремления _к_ гипотенузе, но ведь и верно и другое утверждение: "Для любого епсилон найдется такое N, что расстояние между точками на гипотенузе будет больше или равно епсилон". Или, как уже говорили, для каждого n найдется свой треугольник.
>>> Shedal, спасибо за тёплые слова!
ОтветитьУдалитьНе за что :) А по поводу моих рассуждений ничего не скажете? :)
Sergey, выздоравливайте!
ОтветитьУдалитьShedal, а что можно сказать про Ваши верные рассуждения? ;) Они чёткие и внятные.
Можно разными способами объяснять, почему приведённое "доказательство" некорректно. Главное - понять это для себя. И потом не допускать аналогичной ошибки (неправильного использования мощного инструмента) в других делах, чтобы не наворотить ещё более глупых проблем.
>>Разделяю Ваши опасения про массу некорректных выводов, сделанных без понимания сути.<<
ОтветитьУдалитьЕсли убрать "массу", то это не опасения - я с этим столкнулся. Каждый ученый строит здание своей науки. Редко кто занимается несколькими науками. А кто контролирует строительство? Сами строители. Математика - инструмент всех наук, но математики не контролируют ее применение - это им не интересно. Вот и растет разрыв между достижениями математики и ее применением в других науках, появляются ошибки в теориях. И это никого не волнует.
Сергей, если это не противоречит Вашим обязательствам и представлениям об этичности, могли бы Вы рассказать этот пример, с которым столкнулись? Это было бы очень интересно! Если он длинный, то в комментариях им трудно делиться - тогда приглашаю написать письмо на mytribune AT yandex.ru. Заранее благодарю.
ОтветитьУдалитьP.S. Если он очень узкоспециальный, то, полагаю, его мало кто поймёт. В таком случае, предлагаю не тратить силы на подробное изложение, а показать только схему проблемы.
Чьорт подьери, ведь ответ содержался в самой заметке! И про особенность числа бесконечности, и про неправомерность неаккруатного перехода от частного к общему... Действительно, если утверждение верно для любых сколь угодно больших n, можно распространить это на бесконечность, но не наоборот!
ОтветитьУдалитьМного путей, и все ведут на вершину Фудзи
Но на разные склоны ведут дороги вниз
Будь осторожен, возвращаясь...
abyrvalg, всё верно, ответ лежал на самом видном месте :)
ОтветитьУдалитьЕсть чудная фраза для подобных случаев: "договоримся о терминах". Как только в задаче появляется определение длины - парадокс исчезает.
ОтветитьУдалитьaamonster, если использовать вот это http://ru.wikipedia.org/wiki/%D0%94%D0%BB%D0%B8%D0%BD%D0%B0_%D0%BA%D1%80%D0%B8%D0%B2%D0%BE%D0%B9 определение, то, действительно, "парадокс" исчезает раньше - приравнять сумму катетов к лине никак не удастся, потому что, в соответствие с определением, "...что дуга кривой заменяется ломаной, содержащей точки кривой как точки излома, и максимум длин всех таких ломаных принимается за длину кривой..."
ОтветитьУдалитьЛоманая из катетов содержит точки излома вне гипотенузы, поэтому не может использоваться для определения её длины.
Действительно понятие бесконечности очень сложное и очень сложно представить, что оно собой представляет(также как и понятие нуля).
ОтветитьУдалитьПо задаче:
Так как в задаче встречается понятие бесконечности и для того чтобы быть максимально математически точным и ясным обратимся за помощью к пределам. После дробления сторон треугольника до бесконечности, длина катетов каждого бесконечно малого "треугольника" равна lim a/n=0 где а-сторона исходного треугольника, а n→∞, поэтому сумма всех маленьких кактетов равна n*lim a/n=∞*0. Получаем неопределенность вида ∞*0. Таким образом мы не можем утверждать, что сумма катетов равна гипотенузе даже после проведения бесконечного количества преобразований катетов.
А вот про форму получившейся конечной фигуры, осмелюсь предположить, что получится действительно отрезок представляющий собой гипотенузу (ведь длина гиппотенузы не уменьшалась, а длина катетов в пределе равна нулю).
Уважаемый Автор или придуряется, или жжет или никогда не учил высшую математику.
ОтветитьУдалитьБез умствований для дилетантов скажу, что деля до бесконечности какое нибудь вещество мы придем к микромиру, однако это не значит что тамошние правила действуют для нашей реальности.
Так что
сумма квадратов катетов равна квадрату гипотенузы, причем FOREVER!
Владимир, последняя строчка этой заметки должна снимать все сомнения - «Полагаю, скоро в комментариях появятся подробные объяснения, почему так делать нельзя :)». Да и первые несколько абзацев как раз готовят читателя к тому, что вот-вот будет некорректное доказательство. В этом смысле всё честно.
ОтветитьУдалитьГлавный смысл - научиться искать ошибку в чужом правдоподобном доказательстве. Это очень полезное упражнение.
Мы получим бесконечное количество бесконечно малых величин. Ничего не напоминает? Дифференциалы и интегралами не лезут в голову?
ОтветитьУдалитьВ не зависимости от размеров все правила будут сохраняться. Ведь всегда можно подобрать подобный треугольник, который будет несколько больше.
Я считаю, что тут что-то вроде неправильного понимания предела, где lim1/x=бесконечность, где x->0. Здесь именно предел равен бесконечности, а не выражение 1/0, которое не определено. Так же и lim(sqrt(2)*x), x->0. Такой придел стремится к 0, но не равен ему. То есть он не равен выражению корень из 2 умножить на ноль, хотя очень к нему близок.
ОтветитьУдалитьПредлагаю вариант, при котором ваша формулировка "длина любой стороны треугольника равна сумме длин двух других сторон" являетя верной, причем без всякого подвоха: Необходимое условие- длина одой из сторон треугольника бесконечно мала. Настолько бесконечно мала, что ей можно пренебречь))))))).
ОтветитьУдалитьВо-первых неверно, что если одна линия стремится к другой, то её длина стремится к длине другой. Во-вторых даже в результате бесконечного количества шагов на гипотенузе окажется только счётное множество точек.
ОтветитьУдалить