30 сент. 2009 г.
Интересное в мае
Традиционно предлагаю новым читателям ознакомиться с некоторыми материалами из архива блога - за май этого года. В тот месяц мы много говорили о взаимодействии людей:
1. В заметке «Необходимо, но не достаточно» речь шла о сложностях командной работы. Почему хорошая идея, которая очевидно решает проблему, не находит поддержки у большинства? Есть разные причины. И есть рецепты, позволяющие доводить свою хорошую идею до победного результата.
2. «Загнать себя в угол» - это размышление об осознанном и последовательном ухудшении своих шансов. Иногда это почему-то помогает раскрыться резервам (мол, «отступать некуда»), но иногда приводит к краху.
3. Любите ли вы получать ответ «Я не знаю»? Да, мало кто любит :) Но именно этого ответа часто очень не хватает, потому что получение неверных данных приводит к ошибкам и откладывает правильные действия. Поощряйте откровенный ответ «я не знаю», не гневайтесь на человека, который его даёт, потому что своей честностью он помогает вам раньше найти решение.
Хорошего вам дня!
Запись о заметках прошлых месяцев стала традиционной, поэтому перечислю предыдущие выпуски: интересное в апреле, интересное в марте, интересное в феврале, январе, декабре, ноябре, октябре, сентябре, августе, июле и июне, интересное в первые три месяца жизни блога.
28 сент. 2009 г.
Прямоугольный треугольник наносит ответный удар
Сегодня, глядя на ясный пример, мы лишний раз поймём, что значит мыслить глубоко и зачем нужно хорошее образование. Но сначала кратко объясню смысл прошлой задачки о треугольнике.
Представьте, что специалист освоил какую-то новую технологию, начал ею пользоваться, но иногда производит брак. Вроде бы всё делает правильно, но изредка проскакивает то, чего не должно быть. Если его работа состоит в создании комочков из пластилина, то большой беды не будет. Но если он рассчитывает траектории спутников или принимает решение о необходимости расширения посевных площадей, то такое неуверенное использование технологий не всегда ведёт к успеху.
Поясню, как бывает в некоторых хороших школах:
1) Сначала ученику формулируют свойства биссектрисы и серединного перпендикуляра.
2) Потом ему их спокойно доказывают - идеально, если ученик сам их доказывает, пользуясь редкими, но точными подсказками опытного педагога.
3) И сразу после ему можно говорить: «Ага, раз ты всё освоил, то скорее поехали применять!»
(кстати, если интересно, то могу ещё порекомендовать статью о тонкостях изучения квадратных уравнений)
Выслушав доказательство равенства катета и гипотенузы, ученик, естественно, понимает, что такого быть не может. Но играют с ним не в угадывание, где правда, а где ложь, а в математику :) Он же согласен со всему пунктами доказательства, а не нравится ему только финальный аккорд. Как тогда можно ему доверить применять эти же утверждения о свойствах биссектрис и серединных перпендикуляров, если он в простейшем треугольнике доказывает такой бред?
Если вы ещё не прочитали предыдущую заметку, то предлагаю пока не читать вторую половину этой, потому что вот-вот будет разгадка.
Продолжаем с теми, кто думает, что разобрался с прошлой задачкой :)
Итак, на этом этапе ученик признаёт, что ещё не овладел инструментом, поэтому надо продолжать «копать». Хорошо проводить это в большой аудитории - несколько десятков талантливых ребят начинают хором искать ошибки на всех этапах: одни проверяют корректность признаков, другие - правильность их применения, третьи - пытаются помочь «методом пристального взгляда» изучая чертеж вновь и вновь. И ничего не могут найти.
Но вдруг кого-то неожиданно осеняет: «Биссектриса пересекается с противоположным катетом левее его середины, поэтому точка пересечения биссектрисы и серединного перпендикуляра не может лежать внутри треугольника!»
 «Сейчас исправим» - отвечает опытный преподаватель. И правильно перерисовывает чертёж, повторяя на нём те же рассуждения! И получает тот же вывод - катет равен гипотенузе! Не верите? :)
«Сейчас исправим» - отвечает опытный преподаватель. И правильно перерисовывает чертёж, повторяя на нём те же рассуждения! И получает тот же вывод - катет равен гипотенузе! Не верите? :)Люди мы опытные, поэтому сейчас обойдёмся одним чертежом:
1) Отрезки, соединяющие точку пересечения с вершинами, равны по свойству серединного перпендикуляра - отмечаем это одинарными штрихами.
2) Перпендикуляры, опущенные на стороны угла, равны по свойству биссектрисы - отмечаем это двойными штрихами. И по этому же свойству равны расстояния от верхнего угла до точек его пересечения с этими перпендикулярами - отметим это тройным штрихами.
3) Гипотенуза и катет одного жёлтого треугольника равны гипотенузе и катету другого жёлтого треугольника. Это второй признак равенства, значит жёлтые треугольники равны. И это значит, что их не отмеченные катеты тоже равны - отметим их красными отрезками.
В этот момент уже всё очевидно: и гипотенуза, и катет исходного треугольника равны разности одинаковых отрезков, поэтому равны друг другу. Всё как в предыдущем доказательстве, только точку вынесли за треугольник, поэтому вместо суммы получилась разность.
Возвращаемся к обещанной теме о правильном образовании и глубине понимания: мало сказать «ошибка в том, что точка не может быть внутри треугольника», если это утверждение не решает проблемы. А как мы только что убедились, так и есть - точка легко выдвинулась наружу, доказательство чуть-чуть исправилось, а ошибка осталась. Это и объясняет название данной заметки :)
Кстати, в комментариях к прошлой заметке была сформулирована мысль о том, что выдвижение точки наружу не помогает, что очень ценно!
Почему ценно? Потому что в мире очень много ошибок сделано из-за иллюзии, что «всё уже понятно». А ведь масса проблем имеет несколько причин. Поэтому, найдя одну из них, не всегда надо сразу приниматься за ходьбу по оставшимся граблям. Чтобы не получилось как в анекдоте про ёжиков и филина.
Пожалуйста, напишите в комментариях свой статус по задачке:
1) Легко справился с обоими доказательствами,
2) Легко справился с первым доказательством, но пришлось повозиться со вторым,
3) Сразу понял, где ошибка в первом, но пока не понял, что не так со вторым доказательством,
4) Знал эту задачку (со школы?),
5) Другое.
Хорошего дня!
26 сент. 2009 г.
Прямоугольный треугольник
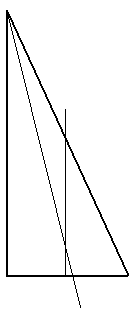
 Сегодня я попробую «доказать» теорему о том, что все прямоугольные треугольники являются равносторонними. Что вообще можно делать с подобными теоремами? Хорошо бы, например, уметь их опровергать. Помните, в разборе парадокса о двух конвертах мы представили ситуацию, которая удовлетворяет условию задачи, но опровергает предположение о том, что вероятности двух конкретных событий равны? Аналогично можно поступить и с данной теоремой - можно предъявить конкретный прямоугольный треугольник со сторонами разного размера (как на рисунке справа). И это полностью опровергнет всю теорему о равенстве сторон любого прямоугольного треугольника. Да и понятно, что слово «доказать» взято в кавычки, потому что хочется лишь создать иллюзию, что доказательство существует и корректно.
Сегодня я попробую «доказать» теорему о том, что все прямоугольные треугольники являются равносторонними. Что вообще можно делать с подобными теоремами? Хорошо бы, например, уметь их опровергать. Помните, в разборе парадокса о двух конвертах мы представили ситуацию, которая удовлетворяет условию задачи, но опровергает предположение о том, что вероятности двух конкретных событий равны? Аналогично можно поступить и с данной теоремой - можно предъявить конкретный прямоугольный треугольник со сторонами разного размера (как на рисунке справа). И это полностью опровергнет всю теорему о равенстве сторон любого прямоугольного треугольника. Да и понятно, что слово «доказать» взято в кавычки, потому что хочется лишь создать иллюзию, что доказательство существует и корректно.Помните, мы недавно разбирали доказательство того, что все лошади одного цвета? Там было неправильное применение метода математической индукции, приводящее к нелепому выводу. И польза такой задачки состоит в появлении дополнительного самоконтроля - теперь, применяя этот метод, человек будет внимательнее, поэтому будет реже обманывать себя по поводу менее очевидных утверждений.
Когда несколько раз проверяешь все пункты доказательства, убеждаясь, что на каждом шаге всё корректно, но итоговый результат очевидно ошибочный, то приходится копаться в себе всё глубже и глубже - а это очень полезно. Почему мы ищем ошибку? Просто из-за того, что хочется понять, как эта простенькая задачка для шестого класса вдруг обводит умного человека вокруг пальца... Ну а если кого-то не обводит, то данное вступление было не для вас :)
 Итак, сначала вспомним пару признаков равенства прямоугольных треугольников, чтобы было на что ссылаться потом:
Итак, сначала вспомним пару признаков равенства прямоугольных треугольников, чтобы было на что ссылаться потом:1) Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
2) Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники тоже равны.
Для краткости я их здесь доказывать не буду. Отмечу только, что первый признак прямо следует из признака равенства треугольников (по двум сторонам и углу между ними), а второй очевиден из теоремы Пифагора - гипотенузой и одним из катетов жёстко задаётся второй катет (обычно его доказывают иначе, но не в этом суть).
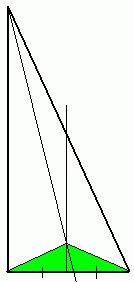 Начнём работать с произвольным прямоугольным треугольником. Возьмём, например, тот, что был на первой картинке. И построим в нём биссектрису из любого острого угла (разделим угол пополам). А из катета, соседнего с другим острым углом, проведём серединный перпендикуляр (перпендикулярную прямую, проходящуюю через его середину). Далее мы построим два отрезка из точки их пересечения - до вершин прямого угла и того острого, который соседствует с данным катетом. На рисунке слева вы можете видеть два зелёных треугольника, равенство которых мы сейчас докажем.
Начнём работать с произвольным прямоугольным треугольником. Возьмём, например, тот, что был на первой картинке. И построим в нём биссектрису из любого острого угла (разделим угол пополам). А из катета, соседнего с другим острым углом, проведём серединный перпендикуляр (перпендикулярную прямую, проходящуюю через его середину). Далее мы построим два отрезка из точки их пересечения - до вершин прямого угла и того острого, который соседствует с данным катетом. На рисунке слева вы можете видеть два зелёных треугольника, равенство которых мы сейчас докажем. Итак, почему же они равны? Это два треугольника, у которых есть один общий катет (значит он у обоих треугольников имеет одну длину). И второй катет - это половина нижнего отрезка, так как мы на нём строили серединный перпендикуляр. Другими словами, два зелёных треугольника равны по первому признаку - у них попарно совпадают длины катетов. Верно? Тогда идём дальше.
Итак, почему же они равны? Это два треугольника, у которых есть один общий катет (значит он у обоих треугольников имеет одну длину). И второй катет - это половина нижнего отрезка, так как мы на нём строили серединный перпендикуляр. Другими словами, два зелёных треугольника равны по первому признаку - у них попарно совпадают длины катетов. Верно? Тогда идём дальше.Из той же точки пересечения биссектрисы и серединного перпендикуляра опустим два перпендикуляра - на гипотенузу и на катет. Получаем ещё два прямоугольных треугольника (рисунок справа). На этот раз мы докажем, что эти голубые треугольники равны.
У них есть общая гипотенуза, поэтому можно попробовать применить второй признак (о равенстве гипотенуз и катетов). Поскольку перпендикуляры опускались из точки, лежащей на биссектрисе, то их длины совпадают по свойству биссектрисы (так как это множество точек, равноудаленных от сторон угла) - данное равенство отмечено одинарными штрихами на чертеже. Получается, что выполнено условие - гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника. Это значит, что голубые треугольники тоже равны.
 Что это нам даёт? Подождите одну секундочку, осталось совсем чуть-чуть!
Что это нам даёт? Подождите одну секундочку, осталось совсем чуть-чуть!Рассмотрим оставшиеся два жёлтых треугольника (на рисунке слева):
Раз зелёные треугольники равны, значит их гипотенузы тоже равны. Но они совпадают с гипотенузами жёлтых треугольников. Это значит, что гипотенузы жёлтых треугольников тоже равны - отметим это на чертеже двойными штрихами.
Ну а раз голубые треугольники равны, то и их катеты равны. Но они совпадают с катетами жёлтых треугольников, поэтому катеты жёлтых треугольников тоже равны (отметим это на чертеже одинарными штрихами).
Выходит, мы опять можем применить второй признак - гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника. Получается, что жёлтые треугольники тоже равны.
 В этот момент уже можно говорить «упс» :)
В этот момент уже можно говорить «упс» :)Если проблема ещё не видна, то предлагаю взглянуть на чертёж справа. На нём отмечены равные стороны жёлтых и голубых треугольников. Хорошо видно, что катет и гипотенуза исходного треугольника состоят из пары одинаковых отрезков. Это значит, что катет и гипотенуза исходного треугольника равны.
Какие это открывает просторы? Огромные! Если один катет равен гипотенузе, то и второй катет тоже равен гипотенузе (по этой же теореме). А это значит, что все прямоугольные треугольники являются равнобедренными - у них равны катеты. А раз оба катета равны гипотенузе, то все прямоугольные треугольники являются равносторонними!
После этого геометрия становится простой и ясной, потому что уж с равносторонними треугольниками мы управимся :)
Повторюсь: я знаю о существовании прямоугольных треугольников с неодинаковыми сторонами, поэтому не надо опровергать данное доказательство словами «доказана глупость, поэтому в доказательстве ошибка». Интересно именно найти эту ошибку :)
Приглашаю обсудить сомнительные моменты доказательства в комментариях (но предлагаю сначала найти своё возражение, а не читать сразу чужие). И очень прошу тех, кто раньше сталкивался с этой задачкой, не рассказывать все секреты, чтобы не лишать остальных читателей удовольствия от самостоятельного разбора. Дело в том, что таких красивых задачек очень мало, поэтому будет очень обидно, если человек, желающий с ней разобраться (и получить от этого себе пользу) не успеет сделать это до того, как кто-то всё объяснит.
Хороших вам выходных!
24 сент. 2009 г.
Банальности и пунктуация
 Если вы любите дух соревнования и стремитесь лучше понимать мысли окружающих людей, то игра «Банальности» вам понравится. Суть очень простая: каждый участник придумывает десять слов, имеющих отношение к текущей теме игры, а потом система считает количество совпадений. Если вы хорошо почувствовали, о чём думает большинство, то набираете много баллов :) Ну а поскольку многие успешно догадываются до типичных мыслей, то часто получается очень интересная и жёсткая борьба за право называться самым банальным.
Если вы любите дух соревнования и стремитесь лучше понимать мысли окружающих людей, то игра «Банальности» вам понравится. Суть очень простая: каждый участник придумывает десять слов, имеющих отношение к текущей теме игры, а потом система считает количество совпадений. Если вы хорошо почувствовали, о чём думает большинство, то набираете много баллов :) Ну а поскольку многие успешно догадываются до типичных мыслей, то часто получается очень интересная и жёсткая борьба за право называться самым банальным.Первый турнир этого сезона пройдет завтра - в пятницу, 25 сентября 2009 в 20.00 Москвы (игра проходит в интернете, поэтому необходимо оказаться у компьютера в это время). Как обычно, из-за тренировки я еле-еле успеваю прибежать к началу :) Рекомендую заранее попробовать сыграть пробный тур (с роботом), чтобы лучше понять суть. Подробнее об игре и пробном туре можно прочитать в ЖЖ fdo.
Теперь к запятым. Юридические документы отличаются многословностью, поэтому легко не заметить в ловко сформулированном тексте запятую на ключевой позиции. Это особенно плохо работает, если заранее иметь (наивное) представление о том, какой смысл сформулирован в данном документе - тогда можно себя неудачно обмануть, неправильно решив, о чём идёт речь.
Недавно один подписчик прислал мне интересный пример - фрагмент текста договора, который он недавно чуть не подписал. Отмечу, что рассматривается обыденная ситуация, вляпаться в которую очень легко - надо просто ходить в магазин и думать о своём будущем. И увидеть выгодное предложение :)
Итак, урезанная часть договора: Прошу передать средства пенсионных накоплений, учтенные в специальной части моего индивидуального лицевого счета, в НПФ [название негосударственного пенсионного фонда], лицензия № [номер] от [дата]., [адрес], а также в последующем ежегодно передавать страховые взносы, которые будут поступать на финансирование накопительной части моей трудовой пенсии в Пенсионный фонд Российской Федерации, в указанный НПФ для формирования им накопительной части моей трудовой пенсии (при отсутствии иного заявления (уведомления)).
Вы поняли, из какого фонда в какой будут переходить деньги? Если у вас есть пара минут свободного времени, то пока не читайте следующий абзац, а определитесь для себя, куда по договору движутся средства.
Может показаться, что в такое длинное предложение нет смысла вчитываться, потому что совершенно очевидно, что негосударственный фонд будет переводить средства в государственный (что вроде бы естественно следует из рекламного обещания). Однако ребус состоит в том, что для такого смысла необходимо поставить хотя бы одну запятую, которой в исходном тексте нет. Другими словами, движение денег по договору будет идти в противоположную сторону, а понять это человек может далеко не сразу (вероятно, получив в следующем году ежегодное уведомление от Пенсионного фонда РФ).
Вроде бы в этом всём нет ничего плохого. Но если человек принципиально хочет отдавать свои деньги только в государственный фонд, а в запятых путается, то он может подписать такой договор. Как будто и нет никакого обмана, так как человек добровольно вступает в договорные отношения, но трудно избавиться от ощущения, что это всё не очень чистоплотно.
Чтобы лучше понять ситуацию с договорами и общей грамотностью, предлагаю вам ответить на вопросы:
Как вы думаете, куда надо поставить запятую в тексте договора, чтобы поменять направление движения средств? Сталкивались ли вы в своей деятельности с подобными юридическими трюками? Как именно вы поняли предложенный фрагмент, когда прочитали его первый раз?
До встречи на пятничных «Банальностях»!
22 сент. 2009 г.
Хаос и английский язык

Периодически я делюсь информацией о хороших фильмах, рассказывая об их особенностях для изучающего иностранный язык. И сейчас я коротко расскажу о сериале, до которого у меня только недавно дошли руки - «House M.D.». Наверное, многие знают, что по сценарию в нём команда врачей спасает людей, больных чем-то непонятным. Но не все слышали, как бодро герои тараторят! Первые серии было очень тяжело смотреть даже с синхронными субтитрами, потому что очень трудно сопоставить мгновенье скороговорной речи и две строки субтитров.
Если в других фильмах, которые мне доводилось смотреть, нормой жизни было «проглатывать» последние буквы слов, то здесь проглатывают слова целиком! :) Кроме того, большое количество медицинских терминов затрудняли понимание первое время. Но к середине первого сезона ухо «приноровилось» - новые слова, означающие всевозможные недуги и ощущения больного человека перестали удивлять, а речь главных героев стала более понятной, что позволило потихоньку начать отказываться от субтитров (увы, до полного их отключения ещё далеко).

Поэтому я рекомендую этот сериал тем, кто хочет потрениировать ухо и набраться новой бытовой лексики (я узнал много новых слов, не имеющих прямого отношения к медицине). Если вы раздумываете, смотреть его или нет, а тем более если вы уже видели этот сериал, то советую глянуть комикс о птицах-хаусах :) Предупрежу, что он содержит несколько моментов, раскрывающих некоторые мелкие внутренние интриги, знание которых кому-то может помешать получить удовольствие от просмотра. Но лично мне он бы не помешал, а здорового смеха точно уже добавил, поэтому рекомендую!
Для успешного обучения важно, чтобы поглощаемый материал был интересным. На занудном тексте/фильме учиться трудно, поэтому переходите от скучного к затягивающему. И ещё важно, чтобы обучение было комфортным: приятнее лежать на диване, а не сидеть на стуле. Ну а чтобы легче было нажимать паузу, перематывать и лезть в словарь за незнакомым словом, рекомендую воспользоваться пультом для компьютера и программой zoomit - она удобно позволяет приблизить нужную часть экрана, чтобы не напрягать зрение и не вставать к экрану.
Ну а под занавес предлагаю доказательство сложности английского языка для одних и необходимости ставить знаки препинания для других - статью с загадочным названием «James while John had had had had had had had had had had had a better effect on the teacher».
Хорошего дня!
20 сент. 2009 г.
Преступная необразованность
и газетах не могут с помощью простейшего
правила отличить случаи, когда следует
писать «тся» и «ться», то как им удаётся
различать демократию и диктатуру?
Если мне правильно процитировали,
то (c) Дмитрий Быков
Разговор сегодня не о знании родного языка, а о непонимании свойств своей психологии. Один хороший знакомый моего родственника несколько лет назад столкнулся с сахарным диабетом у своей шестилетней дочки. Но у него был «бзик» на тему «нельзя садиться на иглу». Причём дело было не в деньгах (он вполне успешный предприниматель), а в принципе. Поэтому он при первой возможности стал снижать назначенные врачами дозы инсулина, попутно общаясь с различными знахарями, которые охотно продавали ему целебные травки, бодро рассказывая, что все беды человечества от уколов.
Мы так устроены, что перед лицом опасности или волшебных перспектив неслабо теряем способность мыслить разумно. Если человеку пообещать завтра вручить миллион, то он сегодня отдаст последнюю тысячу. И только через месяц, когда потеряет надежду найти жулика, он скажет, неожиданно прозрев, что тому, кто знает, где взять миллион, его тысяча не очень была нужна. Другими словами, он знал всё необходимое, чтобы понять, что его обманут.
Аналогично вышло с диабетом: девочку несколько раз привозили в больницу в очень плохом состоянии, врачи её откачивали, пугая родителей обращением в милицию за попытки довести человека до инвалидности. Но знахарское мастерство убеждать и твердолобость родителей ребёнка приводили к повторению сценария: как только они выходили из больницы, опять снижались дозы инсулина, опять необратимо убивалась поджелудочная железа, опять ухудшалось самочувствие. Интересно, что любители самолечения в такой ситуации трезвеют - бегут в больницы, чтобы совсем не потерять жизнь... Хотя только что доверяли совсем другим людям. В тот раз всё «кончилось хорошо» - родители одумались после очередного серьёзного ухудшения состояния дочки. Но зачем маленькому ребёнку такие страдания в возрасте, когда он ещё не может бороться за себя?
В заметке о вероятностях мы говорили об отличии теории вероятностей от многих других наук - она кажется понятной, поэтому хочется довериться своему чутью, а не вникать в достижения специалистов. С медициной ситуация ещё мрачнее: большинство знает устройство человека ещё хуже, чем умеет решать дифференциальные уравнения, но имеет мнение почти обо всём... И нежелание признавать свои ошибки (это тоже свойственно людям) ведёт к тому, что негативные эффекты от заблуждений о здоровье усиливаются в несколько раз. Самые упёртые продолжают пользоваться рецептами целителей даже в том случае, если их уже несколько раз откачивали в реанимации, куда они попали из-за самолечения :(
Почему я об этом вспомнил сейчас? Потому что мне прислали ссылку на раздел форума Первого канала (который «ОРТ»), где обсуждается недавний сюжет «передачи о здоровье» «Малахов+». Там описывается очень похожая история: показали папу с мальчиком, заболевшим год назад сахарным диабетом 1 типа, который «соскочил» с инсулина, назначенного врачом-эндокринологом, слушая господина Малахова и своего родного папу, желающего избавить ребенка от заболевания, делает по 300 приседаний «сжигая сахар» и дышит специфическим «резким» дыханием.
Мне совершенно неважно, настоящие это были люди или актёры. Но если по центральному каналу на всю страну рассказывается, как здорово можно проводить необратимые изменения в организме человека, что по мнению врачей очень рискованно - есть высокие шансы довести человека до смерти или комы (если повезёт, то всего лишь до инвалидности), то что-то не то происходит.
Кстати, эти же центральные каналы сняли пcевдодокументальные фильмы «Плесень» и «Великая тайна воды» (которому какие-то злодеи вручили три премии ТЭФИ, в том числе за лучший документальный фильм, что трудно не назвать вредительством). А на что ещё ориентироваться необразованному человеку? Ему по центральным каналам показывают фильмы, имеющие награды национальной телевизионной премии! Не это ли признак качества информационного продукта для неспециалиста?
Возможно, кто-то меня упрекнёт в напрасном упоре на образованность аудитории, но тут я знаю, что ответить. Человек, имеющий отношение хоть к какой-нибудь науке, меньше верит на слово, меньше поддаётся красивым внушениям, легче замечает логические несостыковки. Нет, он тоже ошибается, но иначе. Итак, три соображения:
1) Нормальный образованный родитель сначала попытается найти информацию о последствиях отказа от инсулина, пообщается с врачами и другими диабетиками (которые расскажут о «придурке, который поверил целителю, а потом его еле откачали в больнице»)...
2) Нормальный образованный родитель ожидает, что существование методики «слезания с инсулина» автоматически означает наличие документа о результатах её тестирования на группе добровольцев. Но поиск информации об этом даёт противоположный эффект - всюду есть описания попыток, которые плохо закончились.
3) Нормальный образованный человек, прочитав о негативных исходах самолечения, поинтересуется, а что будет, если согласиться на инсулин. Оказывается, миллионы людей с сахарным диабетом прекрасно живут, вовремя ставя себе уколы. А раз так, то перед решительными действиями надо всё хорошо выяснить, а не кидаться к первому попавшемуся человеку, обещающему на словах, что всё будет хорошо. Потому что высокие риски при самолечении очевидны (много негативных историй), а риски от нормального лечения почти незаметны.
Другими словами, медицинское образование в таких вопросах - хорошая штука, но и имея просто хорошее образование уже можно не делать откровенных глупостей. Можно ли обвинять человека в том, что он не имеет нормального образования, поэтому верит во всё, что кажется ему полезным? Не знаю. Но можно ли поддерживать того, кто внушает ему теории о возможностях лечения, применение которых, с точки зрения медицины, может привести к необратимым изменениям (например, смерти)?
P.S.
Нашлись люди, которые утверждают, что подали заявление в прокуратуру. Поглядим.
18 сент. 2009 г.
Признаки Skynet
 Итак, во-первых, музыкальная группа «386DX» - прекрасная реализация чудовищной идеи (шучу :)
Итак, во-первых, музыкальная группа «386DX» - прекрасная реализация чудовищной идеи (шучу :)Представьте, что какие-то люди научили компьютер петь песни (обычным синтезатором речи), воспроизводить музыку (банальное MIDI) и выводить адекватный всему этому видеоряд... Вроде бы ничего сложного, хоть и не так очевидно, зачем это всё надо.
А теперь представьте, что этот 386-ой компьютер (авторы справедливо рассудили, что для такой задачи более мощная машина не требуется) выступает в различных клубах, поёт на Арбате, выпустил два компакт диска («Легенда русского рока» и «386 DX. the best of»), снял два видео-клипа... Это настоящая звезда (с четырьмя мегабайтами оперативной памяти :)
Кстати, очень рекомендую прочитать на сайте группы тексты о том, как это всё делалось - детали реализации мне показались весьма интересными (внятно описано, что всё далеко не просто). А главное во всём этом то, что наглядно показано, что слабенький компьютер и талантливый человек могут создать уникальную вещь, а профессиональная студия с мощным оборудованием и много слабой молодёжи способны только забивать эфир мусором.
 Во-вторых, появились самопечатающие принтеры. Сначала поясню для тех, кто не сталкивался ранее с 3d-принтерами - уже относительно давно при разработке различных изделий начали использоваться трёхмерные принтеры (печатающие трёхмерное изделие по его описанию). Удивительно наблюдать, как такое устройство создаёт цепь (пластиковую цепь с отдельными круглыми звеньями!) по только что нарисованной в специальном редакторе модели.
Во-вторых, появились самопечатающие принтеры. Сначала поясню для тех, кто не сталкивался ранее с 3d-принтерами - уже относительно давно при разработке различных изделий начали использоваться трёхмерные принтеры (печатающие трёхмерное изделие по его описанию). Удивительно наблюдать, как такое устройство создаёт цепь (пластиковую цепь с отдельными круглыми звеньями!) по только что нарисованной в специальном редакторе модели.А недавно я прочитал о реализации ещё более мрачной штуки: устройство, которое способно создать 60% компонентов самого себя (а остальные 40% - это простые и дешёвые детали, которые легко купить в соответствующем магазине). Кстати, это соотношение интересно коррелирует с человеческими способностями - организм также может производить 60% аминокислот, а остальное получает из окружающей среды. Пока что это просто интересное бизнес-соображение - если организации надо 10 принтеров, то она может купить один, а остальные девять напечатать. Но надо понимать, что роботы уже почти научились размножаться! Понимаете масштаб трагедии? :)
 И последнее - для своих грязных целей они используют человеческие мозги. Мощный компьютер отличается от слабого человека тем, что не имеет интуиции. Опытный человек чувствует, какие ветки решения стоит пробовать, а что отложить на потом, но очень редко может формализовать это в компьютерной программе. И поэтому вычислительным устройствам приходится проводить огромный перебор, чтобы достичь того результата, который человечек сразу «видит».
И последнее - для своих грязных целей они используют человеческие мозги. Мощный компьютер отличается от слабого человека тем, что не имеет интуиции. Опытный человек чувствует, какие ветки решения стоит пробовать, а что отложить на потом, но очень редко может формализовать это в компьютерной программе. И поэтому вычислительным устройствам приходится проводить огромный перебор, чтобы достичь того результата, который человечек сразу «видит».Но человеческому интеллекту не долго осталось главенствовать - его можно использовать ещё проще, чем колесо или рычаг. Всё легко - людям нравится играть? Нравится. Поэтому надо предложить играть этим носителям сверхмощных природных компьютеров на своих бездарных плечах. Но не просто играть, а решать нужные задачи, которые крайне трудно одолевать перебором (например, задачу о трёхмерной структуре белка). В данном случае сделано всё: подготовлены дистрибутивы для трёх самых распространённых операционных систем, разработано внятное объяснение, как сворачивать белки можно, а как нельзя, введена система рейтингов... И всё! Тысячи людей бросились тешить своё самолюбие, набирая баллы за сборки простейших белков. Как только человек осваивается, ему хочется подняться в таблице выше - для этого надо справиться с ещё не решённой задачей, над которой бьются многие биологи... Но разве это остановит? ;)
Компьютеры переложили на людей свою работу (решать задачи), но научились петь рок и размножаться (чем традиционно занимались люди). Что-то поменялось в этом мире :)
Хороших вам выходных! Размножайтесь ;)
16 сент. 2009 г.
Слишком универсально
Теперь вопрос: позволяет ли это производителю снизить цену на товары нижнего уровня? Нет, потому что он сначала делает именно полноценное устройство, обладающее всеми функциями (а себестоимость от сокрытия нескольких функций не падает). Это означает, что производитель таким образом может только повысить цену на товары верхнего уровня.
Поэтому знающие люди покупают минимальную модель за разумные деньги, а потом дома отключают у неё лишние ограничители возможностей - так они лишаются гарантии производителя, но получают качественный товар за разумную цену (иногда это получается случайно - провайдер не смог урезать мне доступ к услуге, поэтому я плачу меньше, но не имею возможности требовать работоспособности, если что-то поломается).
А бывает так, что производитель даёт доступ к очень мощному инструменту. Такому мощному, что даже профессионал может легко совершить ошибку, потому что уж очень много кнопок позволяют влиять на процессы. Больше того, если мы используем сложный инструмент для простой задачи, то помимо трудностей с настройкой и управлением, мы получаем неожиданный антибонус - все минусы мощного устройства. На своём месте они казались приемлемыми, потому что мощная и универсальная технология давала массу преимуществ. Но страдать от тех же минусов при решении простой задачи - это слишком дорого.
Простой пример - многие современные осциллографы работают под управлением операционной системы Windows, поэтому приходится тратить много сил, чтобы понять, где именно проблема: в физическом устройстве, которое должно давать сигнал, в программном обеспечении осциллографа, в операционной системе, которая решила проявить самостоятельность или в перегреве каких-то компонент компьютера, на котором это всё работает. Чем проще устройство, тем меньше у него причин сломаться.
Но давайте рассмотрим самое простое и распространённое: цикл for в C-подобных языках программирования. Если я заранее предупрежу, что ниже есть ошибка, то Вы её легко найдёте:
int i, j;
for (i=0; i<10; i++) {
for (j=0; i<10; i++) {
// ... сложный код
}
}
Но представьте, как долго её можно искать, если вокруг есть много сложного кода. В чём же проблема? Кто-то скажет, что надо запретить использовать copy-paste в средах для разработчиков, чтобы не порождать подобных ошибок, кто-то скажет, что бывают компиляторы, предупреждающие об изменении переменной цикла внутри тела цикла, а кто-то будет утверждать, что у него точно таких ошибок не бывает, потому что он внимательный. Ещё есть понятные соображения про итераторы и более осмысленные имена переменных... Но когда мне пришлось исправлять код, который почти всегда работает правильно (потому что почти всегда в первой строке таблицы был элемент с нужными свойствами, что приводило к успешному прекращению цикла), то найти ошибку было нелегко. Хотя сама ошибка очень простая - скопировав строчку, программист исправил имя переменной только один раз, а не три (видимо, отвлёкся).
Есть языки программирования, синтаксис которых не требует трижды указывать имя одной переменной, если необходимо перебрать целые значения от одной величины до другой (я думаю, вы согласитесь, что это самое распространённое применение цикла for). Их ограниченная спецификация не позволяет делать некоторые интересные трюки, которые легко удаются C-программистам, но она не позволяет делать таких ошибок. Полагаю, это хороший пример слишком мощного инструмента, приглашающего наделать глупых ошибок, который крайне редко используется в полную мощь. Кстати, некоторые участники олимпиад по программированию используют специальные макросы вида «FOR(i,a,b)», которые автоматически раскрываются в конструкцию «for(i=(a);i<(b);i++)» - это позволяет быстрее реализовывать простой код, заведомо избегая подобных распространённых граблей.
Вспоминается по этому поводу история, которую рассказывал Терехов Андрей Николаевич - генеральный директор ТЕРКОМ. Когда он только начинал делать программно-аппаратные комплексы для различных военных задач, ему довелось участвовать в обсуждении установки, которую создали за многие годы до того разговора. И он произнёс довольно резкие слова по поводу производительности той системы - «как же так надо было проектировать, что включение установки и её подготовка к работе происходят целых полторы минуты?». На что неожиданно отреагировал очень взрослый и опытный конструктор (как оказалось, это был создатель обсуждаемого комплекса): «Во-первых, личный состав по нормативам должен успевать приготовиться к выполнению боевой задачи за две минуты, поэтому старт за полторы - это вполне достаточно, а во-вторых, попробуйте сначала сами сконструировать систему, которая будет надёжно работать в боевых условиях» (если я правильно помню, то вычислительное устройство могли монтировалось на ГАЗ-66 и БМП, подвеска которых не отличается мягкостью).
В такой момент приходит понимание, которое у военных есть всегда - делать надо не что-то идеальное и универсальное, а то, что решает поставленные задачи и имеет высокую надёжность. Андрей Николаевич говорил, что у него после этих слов более опытного коллеги многое в голове встало на место.
Вывод: слишком универсальные решения бывают, причём они имеют как минимум два минуса:
1) они могут быть слишком сложными, поэтому будут плохо выполнять свою функцию (компьютер с тв-тюнером может полностью заменить видеомагнитофон, но сможет ли им пользоваться ваша бабушка?),
2) ради расширения функциональности приходится заметно поднять цену (да, компьютер с тв-тюнером может автоматически вырезать рекламу, может самостоятельно скачивать программу передач и ещё много всего, но он стоит в 10 раз дороже видеомагнитофона).
Совершенно нет разницы, название какой компании написано в графе «производитель», какие конкурсы назвали его «товаром года», в каких журналах его называют передовым и уникальным. Важно только то, как оно работает - хорошо выполняет свои функции или плохо. И ирония нашего времени состоит в том, что производителю выгодно делать хорошие вещи, а потом их портить. Что-то не так в мире, если к экономическому росту приводит быстрое преобразование природных богатств в кучи мусора на свалках (у нас ведь только рост потребления ведёт к оздоровлению экономики?). Кстати, только что взглядом на это поделился Макс Крайнов - он предлагает посмотреть на вопрос стимулирования экономики не с позиции банкиров и промышленников, а исключительно со своей колокольни. Поскольку потребитель указывает производителю, что делать (покупая или отказываясь от каких-то товаров), то можно надеяться, что распространение вменяемого отношения к навязываемой необходимости постоянно что-то покупать сможет стимулировать производителей и продавцов делать правильные шаги.
Хорошего вам дня!
13 сент. 2009 г.
Разбор осей симметрии
Но мне интересней другой аспект этого вопроса. Все люди разные, поэтому могут видеть отличающиеся вещи, глядя на одну сущность. И поэтому очень интересно «влезть в шкуру» - понять, что и почему думает другой человек. Это не только очень увлекательно само по себе, но и позволяет лучше понять процессы внутри себя. Да и других людей понимать бывает очень полезно (об этом вчера была опубликована история про аптеку). Другими словами, хоть мозг и плохо подходит для изучения мозга, ничего лучше мы пока не нашли, поэтому будем пользоваться им :)
Просто так за людьми можно долго наблюдать, но огромный поток получаемой информации очень затрудняет вычленение критически интересных моментов. Поэтому меня привлекают простые задачки, про которые уже известно, что они у многих вызывают коллизию интуиции и рациональности (после заметки я приведу ссылки на некоторые из ранее рассмотренных примеров). На них быстро выявляются (или не выявляются) интересные сложности, которые заставляют глубже задуматься о понимании других людей.
Итак, разберёмся наконец с задачкой о квадрате и осях симметрии, это очень полезное упражнение по изучению объектов чужими глазами.
Какие бывают ответы и как их получить:
Ответ 1. Если пристальный взгляд на картинку даёт только квадрат с координатами (-1,1), (1,1), (1,-1) и (-1,-1), то это обычно означает одно из двух:
1) невнимательное чтение задачки (делалась попытка найти квадраты, у которых оси симметрии совпадают с обоими осями координат, хотя достаточно было одной оси).
2) расслабленность при решении.
Ответ 3. Это очень распространённый ответ, выдающий внимательного человека, который очень верит своей интуиции, а на грабли наступает редко :)
Быстрый мозг подсказывает, что к квадрату из первого пункта стоит добавить ещё два:
(а) (-1,1), (-1,-1), (-3,-1), (-3,1) и
(б) (-1,1), (1,1), (1,3), (-1,3).
Это сдвиги исходного квадрата вдоль каждой из осей координат, при которых одна сторона квадрата переходит в другую. Увы, после этого часто возникает ощущение, что дальше копать некуда: двигать дальше по осям бесполезно, так как точка (-1,1) перестаёт быть вершиной квадрата, значит считаем задачу решённой. Были комментарии «могу доказать, что 3 - максимум» и «почему я вижу только три?» (видимо, после прочтения чужих комментариев), что подтверждает возникновение стойкого внутреннего ощущения, что дальше копать некуда, поэтому другие квадраты найти не удаётся или очень трудно.
Ответ 6. Я знаю два способа получить такую версию:
1) Проводим рассуждение для каждой из осей X и Y. Сначала разберёмся с осью X: если точка (-1,1) является вершиной квадрата, то симметричная относительно оси X точка (-1,-1) тоже будет вершиной квадрата. Получается, мы уже имеем две вершины - осталось понять, какие две ещё могут быть. Но тут просто: отрезок между этими двумя вершинами может быть правым ребром квадрата, левым ребром или диагональю. Для оси Y аналогично находим ещё 3 квадрата. Получается, что всего их 6. Это решение во многом неплохое, но выдаёт некоторую невнимательность.
2) Другое решение аккуратнее. Мы замечаем, что в двух найденных наборах из трёх квадратов есть два одинаковых, поэтому понимаем, что в плоскости XY квадратов может быть ровно 5 (и я это называю правильным решением). Но тут возникает идея выйти из плоскости. Пусть одна диагональ шестого квадрата будет идти из точки (-1,1) в (1,-1), а вторая диагональ будет на оси Z: одна точка на корень из 2 выше нуля, а другая - на корень из 2 ниже. Получается опять 6 квадратов. Здесь, как я понимаю, мозг думает примерно следующее: «ага, я увидел этот трудный повёрнутый квадрат, сложнее ничего не бывает, поэтому задача решена».
Ответ 7. Здесь рассуждения аналогичны: найдя 5 квадратов на плоскости, продолжаем искать что-нибудь в объёме. Например, можно взять квадрат, перпендикулярных оси X, у которого центр находится на оси X, а одна из вершин имеет координаты (-1,1,0). Получаем квадрат (-1,1,0), (-1,0,1), (-1,-1,0), (-1,0,-1). Аналогично для второй оси.
Ответ 8. Комбинация предыдущих двух: добавили к 7 квадратам один диагональный (с вершиной (0,0,sqrt(2)).
Ответ 9. К тем 7 квадратам, что нашли выше, добавили ещё два, проходящих через ось Z: один с верхним ребром (-1,1)-(1,-1), а другой с таким же нижним ребром. Удивляет, что при этом не нашли квадрат с такой диагональю :)
Ответ 4. Всё делаем как в первом случае «ответа 6» (разбираем ситуацию для обоих осей отдельно), но не замечаем возможности построить повёрнутые квадраты, поэтому имеет ответ 4, а не 6.
Ответ бесконечно много. Распространены два способа получать такой вариант. Один будет рассмотрен чуть позже, а второй состоит в неправильном понимании термина ось симметрии (если считать осью симметрии такую прямую, которая делит фигуру на две равных).
Если вы получали другие ответы интересным образом или эти же ответы, но существенно другими способами, то, пожалуйста, напишите об этом в комментариях - это интересно!
Какой ответ правильный? Я не думаю, что это очень важно. Я бы считал правильным ответом 5, потому что все выходы в трёхмерное пространство странны тем, что мы не пошли дальше - в четырёхмерное и так далее (тогда бы легко получили бесконечное множество квадратов, которое иногда предлагалось в качестве ответа в комментариях прошлой заметки). Разговоры о недоопределённости задачи я понимаю, но в данный момент не считаю интересными.
А вообще, это была задачка для 9-10 класса математического конкурса Кенгуру (2004 год, задача номер 16). Кстати, сам проект очень рекомендую! Поскольку баллы, набранные при решении задачек, ни на что не влияют, то и конкурсом этим не интересуются различные коррупционеры и прочие товарищи, меняющие дух интеллектуального соревнования детей на измерение кошельков родителей. Если у вас подрастают детки, то я рекомендую дать им возможность поучаствовать в таком мероприятии - это очень интересно, но стоит каких-то символических денег. Хоть это и тест с вариантами ответов, там есть интересные задачки, способные не только померить знания ребёнка, но и научить новому (список задачек).
По причине школьного уровня этой задачки я предлагал уделить ей не больше 1-2 минут. В полном варианте предлагается 30 задач, работа длится всего 75 минут, а вопрос о квадрате был не самым сложным. Поздравляю всех, кто решил её правильно! (большинство ответов было 5)
Обещанные ссылки на заковыристые задачи:
1. Характерная алгебраическая задачка - если не знать заранее, что она не просто так, то ошибка будет с очень высокой вероятностью. А если знать, то просто с высокой :)
2. Задачка о двух конусах тоже заманивает в несколько разных способов получить неправильные ответы (для неё был проведён аналогичный разбор, который лучше не читать до самостоятельного решения).
3. Задачка о 8 монетах тоже всеми конечностями толкает к неверному ответу, так что нелегко удержать себя от поспешных заявлений о своём варианте решения :)
А какие интересные задачки с похожими сбоями трезвого мышления знаете вы?
10 сент. 2009 г.
Ещё раз о вероятностях
только затем, чтобы им удивляться;
Любознательный же - затем, чтобы
узнать их и перестать удивляться.
Рене Декарт
Две недели назад мы разбирали парадокс двух конвертов (более 100 комментариев - я надеюсь, все желающие всё поняли). А сегодня я предлагаю короткий разговор о понимании теории вероятностей (с ясным примером). И в последнем абзаце будет забавная задачка.
Итак, сначала о теории. Отличие теории вероятностей от большинства других наук состоит в том, что она реально кажется понятной (поэтому, вроде как, её и не надо сильно изучать - разумному человеку всё и так будет ясно, а учёные навыдумывали себе сложных теорем, которые никому не нужны). Поэтому многие люди, которые математическую задачу последний раз пытались решать очень давно, не просто имеют мнение о конкретной задачке из теории вероятностей, а убеждены в своей правоте (ещё бы, они же имеют здравый ум и рационально мыслят!) Представьте, что кто-то принесёт аналогичный парадокс про решение дифференциального уравнения или о задачке из ТФКП. Да это никто не станет публиковать и обсуждать! Потому что данные научные дисциплины большинству совсем неизвестны. А про теорию вероятностей многие готовы высказаться.
Представьте, что кто-то принесёт аналогичный парадокс про решение дифференциального уравнения или о задачке из ТФКП. Да это никто не станет публиковать и обсуждать! Потому что данные научные дисциплины большинству совсем неизвестны. А про теорию вероятностей многие готовы высказаться.
Пример - на Хабре опубликовалась статья Гослото — государственная лотерея по-русски!. Идея очень простая - автор проанализировал выигрышные комбинации с начала года, обвёл красным числа, идущие подряд в натуральном ряду (например, 34 и 35), обвёл синим числа, идущие через одно (например, 11 и 13), после чего заявил: «Теория вероятности отказала и больше не работает. Вероятность выпадения тиража с соседними числами стремиться к 1. Ваши выводы, Россияне?» (на картинке справа видно, что в очень многих строчках есть числа, обведённые цветными кружками).
И знаете, если люди хотят видеть плохое, а здесь «всё так очевидно», то они начинают поддерживать автора, не разобравшись. Следом идут такие комментарии: «даже эти палятся», «рандомайзер хреновенький выбрали по ходу», «может шары прилипли?», «забыли RANDOMIZE TIMER» (приношу извинения, если кого-то обидел, цитируя комментарии в таком тоне).
Конечно, хабровчане быстро во всём разобрались - нашлись люди, дружащие с теорией вероятностей, которые тут же прикинули, что соседние числа в тиражах как раз должны быть очень часто (а если бы они наоборот были редко, то это наводило бы на мысли о какой-то хитрости). На эту тему есть очень наглядный Парадокс дней рождения, обычно формулируемый так: «вероятность того, что в случайной группе из 23 человек хотя бы у двоих дни рождения (число и месяц) совпадут, больше 50%». Интуиция подсказывает, что это событие очень маловероятно, но честные вычисления дают ещё более удивительные факты: в группе из 30 человек найдётся двое с одной датой рождения с вероятностью 70%, а в группе из 55 человек - с вероятностью 99%! Заметьте, что 99% отличается от 100% совсем чуть-чуть, а количество людей - 55 от 366 - отличается в 7 раз. Поэтому сразу удивляться от высокой частоты соседних чисел в лото очень наивно. Достаточно посмотреть, как близко расположены дни рождения у коллег или одноклассников, чтобы заподозрить свою интуицию в недобром :)
Я опасаюсь школьного курса теории вероятностей до специального курса для учителей из-за широкой распространённости применения «здравого смысла» без знания. Если преподаватели будут понимать науку на бытовом уровне, но станут учить ей, то через поколение у нас будет много людей, которых «в школе научили, поэтому они сейчас точно знают» (не имеют фактического знания, но уверены в себе ещё больше, потому что имеют пятёрку в аттестате по этому предмету, грубо говоря). На этом торжественно обещаю прекратить на некоторое время обсуждения проблем с вероятностями :)
Теперь обещанная школьная задачка: сколько существует квадратов с вершиной A(-1; 1), для которых хотя бы одна из координатных осей является осью симметрии? Пожалуйста, через 1-2 минуты напишите в комментариях свой ответ - одну цифру от 1 до 9, не читая чужих версий (конечно, не пишите решение, оставьте только ответ). А в следующей заметке я объясню, зачем всё это ;)
8 сент. 2009 г.
Кто, кто в интернете живет?
 Широко отмечать не будем, но некоторый анализ ситуации сделать можно. Начнём с русского сегмента интернета вообще. Вооружившись данными liveinternet.ru, мы получаем интересные картинки: на графиках отображены доли пользователей определённых браузеров и операционных систем в разные дни.
Широко отмечать не будем, но некоторый анализ ситуации сделать можно. Начнём с русского сегмента интернета вообще. Вооружившись данными liveinternet.ru, мы получаем интересные картинки: на графиках отображены доли пользователей определённых браузеров и операционных систем в разные дни.Легко видеть, что по выходным дням доли пользователей Windows XP и 2000 снижаются, но вырастают Vista и Windows7. Объяснения понятны: у многих на рабочем компьютере стоит старая проверенная система для работы, а дома - новые эксперименты и предустановленные системы. Ещё заметнее колеблются вокруг выходных дней браузеры: резко падает IE6 (заметьте, как его много на рабочих машинах!), слегка проседает IE7, но подпрыгивают Firefox3 и Opera9. Кстати, на графике хорошо видно начало миграции с девятой Оперы на свежую десятку. Почему в офисах так много IE? В некоторых компаниях предполагается работа сотрудников через веб-интерфейс, причём сайт выполнен с элементами ActiveX (работают только в IE), поэтому пользователи изначально вынуждены пользоваться этим браузером. Но многие всё же просто не знают отличий браузеров, потому что видели в своей жизни только один InternetExplorer (хотя IE6 и IE7 имеют известные уязвимости). Впрочем, пользователям других браузеров тоже не надо расслабляться.
Зачем всё это? Чтобы было с чем сравнивать! Я выделяю три типа сравниваемых пользователей:
1) все пользователи русского сегмента интернета (посчитанные liveinternet.ru),
2) посетители блога «Привычка не думать» две недели назад,
3) посетители блога «Привычка не думать» сейчас (после существенного пополнения хабровчанами).
Например, доли пользователей WindowsXP в этих категориях такие: 74%, 77%, 65% (заметно упала для блога). Доля висты тоже падает: 13%, 13%, 10%.
Подтвердилось то, что хабравчане - любители всего нового, так как Windows7 рванула вверх: 2%, 2%, 10%. И любят надёжность и предсказуемость - доля Unix'а серьёзно подскочила: 0.5%, 3%, 10%. Ну и приверженцев Apple тоже добавилось: 0.5%, 1%, 3%.
Что же видно по браузерам? Я давно радовался тому, что подписчики блога заметно реже используют ненадёжные и неудобные браузеры, чем в среднем по интернету. С приходом аудитории Хабрахабра соотношения только усилились :)
Растут:
- Firefox3: 22% -> 35% -> 40%
- Opera10: 5% -> 3% -> 13%
- Chrome: 2% -> 5% -> 15%
- Safari4: 0% -> 1% -> 2%
- Opera9: 19% -> 20% -> 15% (перетекает в Opera10)
- IE7: 20% -> 15% -> 5%
- IE6: 14% -> 6% -> 2%
- IE8: 8% -> 8% -> 2%
 Распределение по странам не поменялось, а с городами выявился интересный эффект - за последнее время с 10% до 20% поднялась доля читателей из Санкт-Петербурга (приветствую культурную столицу!).
Распределение по странам не поменялось, а с городами выявился интересный эффект - за последнее время с 10% до 20% поднялась доля читателей из Санкт-Петербурга (приветствую культурную столицу!).Теперь вы тоже видите примерные черты других читателей этой записи. Согласитесь, замечательная компания собралась!
Ещё есть сомнительная информация о примерном распределении полов и возрастов. Я плохо представляю, как liveinternet.ru добывает эти данные, поэтому не считаю, что им можно доверять. Они утверждают, что доля мужчин старше 20 лет поднялась в полтора раза (с 60% до 85%), тем самым вытеснив женщин (30% -> 10%). Результат чудовищный, потому что без женщин никак нельзя :) Поэтому я предлагаю в эти данные не верить, но пригласить на блог женщин, которым это может быть интересно :)
Хорошего дня и до новых встреч! Кстати, в следующий раз будет задачка.
6 сент. 2009 г.
А пусть не пишет!
-Чтобы мел не писал.
-Но зачем?
-А пусть не пишет!
-Хорошо, но зачем, чтоб не писал?
-А пусть не пишет!
 Это совершенно нормально, что людям нравится ощущать свою правоту. Я думаю, это заложено в защитные механизмы, сформированные очень давно. «Если я прав, значит я всё понимаю и контролирую, значит я в безопасности» - естественный ход древней мысли. Неправому же человеку не очень комфортно: он ощущает свою малую осведомлённость, чувствует свою уязвимость - ему страшно.
Это совершенно нормально, что людям нравится ощущать свою правоту. Я думаю, это заложено в защитные механизмы, сформированные очень давно. «Если я прав, значит я всё понимаю и контролирую, значит я в безопасности» - естественный ход древней мысли. Неправому же человеку не очень комфортно: он ощущает свою малую осведомлённость, чувствует свою уязвимость - ему страшно.
Сегодня я расскажу три автомобильных истории, которые, похоже, построены на нежелании признавать свою неправоту.
На прошлой неделе я, как обычно, возвращался домой на велосипеде. Дорога знакомая, достаточно широкая, еду свои 30-35 км/ч, не создавая помех обгоняющим автомобилям (на том участке дороги ограничение скорости - 40 км/ч и запрещён обгон). Метрах в пятидесяти передо мной пересечение со второстепенной дорогой, там стоит автомобиль, выражающий своё желание повернуть налево, но встречный поток пока плотный, поэтому ему некуда выезжать. В какой-то момент у меня создаётся впечатление, что мы встретились взглядами с водителем выезжающего автомобиля - я разгледел напряжённое выражение лица и шевеление губ (он что-то произносил, хотя пассажиров в салоне не было). И вдруг он неожиданно разгоняет свой красный автомобиль прямо во встречный поток. Визг тормозов, одна из машин, стараясь уйти от столкновения, заезжает на тротуар (благо, там никого не было в тот момент), остальные имеют возможность экстренно остановиться. К счастью, никто не пострадал. Водитель красного автомобиля тут же уехал, остальные после небольшой паузы тоже продолжили движение. В другой раз было весьма похоже - автобус стоял на остановке, а слева от него шёл плотный поток машин (скорость была около 40-50 км/ч, так как перед этим был медленный поворот, я же разогнался до 25-30). Формально водители обязаны выпустить автобус из остановочного кармана, так как он включил сигнал поворота. Но поток машин шёл непрерывный, поэтому я тоже решил проехать (всё равно автобусу придётся стоять, пока не образуется достаточного окна). Дальше произошло совершенно неожиданное - как только я подъехал близко к автобусу, он дёрнулся в едущий слева от него поток машин. Благо, у всех хватило реакции: автомобили, двигающиеся слева от автобуса, резко сместились влево, а водители встречного направления мгновенно дали им место, влетев колёсами своих машин в бордюры. Это были очень опасные манёвры, но никто не пострадал.
В другой раз было весьма похоже - автобус стоял на остановке, а слева от него шёл плотный поток машин (скорость была около 40-50 км/ч, так как перед этим был медленный поворот, я же разогнался до 25-30). Формально водители обязаны выпустить автобус из остановочного кармана, так как он включил сигнал поворота. Но поток машин шёл непрерывный, поэтому я тоже решил проехать (всё равно автобусу придётся стоять, пока не образуется достаточного окна). Дальше произошло совершенно неожиданное - как только я подъехал близко к автобусу, он дёрнулся в едущий слева от него поток машин. Благо, у всех хватило реакции: автомобили, двигающиеся слева от автобуса, резко сместились влево, а водители встречного направления мгновенно дали им место, влетев колёсами своих машин в бордюры. Это были очень опасные манёвры, но никто не пострадал.
Возможно, я преувеличиваю желание некоторых водителей показать своё главенство на дороге (выглядело всё так, как будто их главная цель - не пропустить велосипедиста перед собой). Чем-то другим столь опасные действия автомобилистов тоже объяснить можно: водитель красного автомобиля из первого примера мог безумно спешить (и говорить в момент выезда по телефонной гарнитуре с человеком, который его торопит), а водитель автобуса мог просто не заметить множество автомобилей, которые он чуть не снёс...
Можно находить разные объяснения. Но мне кажется, что версия с позицией «докажу, что он ошибается» имеет право на существование. Впрочем, давайте рассмотрим исключительно автомобильное ДТП, в котором всё было чётко замерено и доказано. На «Правильном водителе» опубликован разбор ДТП, в котором грузовой автомобиль сместился в чужую полосу, спровоцировав ДТП. Тонкость в том, что водитель грузового автомобиля утверждал, что не мог предвидеть аварии, а виноват во всём водитель соседней машины, который неправильно рассчитал траекторию. Однако замеры инспекторов ГАИ показали, что виноват именно водитель грузовика.
Мораль в том, что если человек выдумал себе теорию, то он часто будет стараться поддерживать её жизнь, даже если это противоречит разуму. В первых двух случаях водители могли подумать, что «велосипедист медленный, он не успеет доехать, поэтому я его не пропущу» - а о других участниках движения не подумали вообще (потому что изначально так не любят велосипеды на дороге, что забывают обо всём). В последнем случае водитель грузовика подумал, что легковая машина не сможет проскочить, но для надёжности сместился так, чтобы она и впрямь не смогла (дабы оказаться правым в своей теории).
Велосипедистам же на дороге надо не только знать ПДД, но и постоянно ожидать различных некорректных действий (некоторые водители специально выражают своё чувство превосходства, подрезая и опасно прижимая велосипедистов к бордюрам).
Будьте осторожны и берегите себя!
3 сент. 2009 г.
Наши суши хороши
 Последние годы популярность суши-баров и сервисов по доставке суши на дом очень выросла, но не все любят питаться вне дома, а предпочитают заведомо качественную и не очень дорогую домашнюю еду. Да и делать что-то своими руками всегда приятно - потом долгое время можно радоваться своей работе. В случае с едой, конечно, не очень долгое время :)
Последние годы популярность суши-баров и сервисов по доставке суши на дом очень выросла, но не все любят питаться вне дома, а предпочитают заведомо качественную и не очень дорогую домашнюю еду. Да и делать что-то своими руками всегда приятно - потом долгое время можно радоваться своей работе. В случае с едой, конечно, не очень долгое время :)Поэтому сегодня я расскажу о приготовлении простого и вкусного блюда. Нам понадобится:
Оборудование
1.Коврик для суши - не обязательно брать специальный бамбуковый, можно самый простой (200-300 рублей),
Основа - незаменимые компоненты
2. Водоросль нори (5 рублей за лист),
3. Круглозёренный рис - подойдёт рис для ризотто, но можно взять и специальный рис для суши (100-150 рублей за килограмм),
4. Уксус - желательно рисовый, так как у него более мягкий вкус,
Начинка - можно комбинировать произвольно, расширяя свой список по вкусу :)
5. Филе красной рыбы - сёмга, горбуша, лосось, форель, тунец (ниже о ней будет более подробный разговор),
6. Можно использовать крабовые палочки, заправленные майонезом - вкусно и дёшево,
7. Свежий огурец,
8. Сливочный сыр - «Филадельфия»/«Buko»/...,
9. Авокадо,
...
Приправы и соусы - тоже по вкусу :)
10. Соевый соус,
11. Васаби,
12. Маринованный имбирь.
И всё! Осталось приготовить, что очень быстро и весело:
1. Промываем рис, варим его (обычно рис и вода берутся в соотношении 1 к 2 по весу), после чего заправляем подсоленным и подслащённым уксусом, даём рису остыть,
2. Оборачиваем коврик для суши пищевой плёнкой - так в него не будет забиваться пища,
3. Кладём на коврик лист нори, сверху распределяем рис, постоянно смачивая руки в уксусной воде, чтобы не прилипал,
4. Выкладываем начинку - пробуя разные комбинации ингредиентов, чтобы выбрать самые удачные,
5. Сворачиваем коврик со всем, что на нём есть - получаем колбаску,
6. Если ещё остался рис, то переходим к шагу 3. Если рис кончился, то идём дальше.
7. Разрезаем все подготовленные колбаски (роллы) на 8 частей (удобно делать это методом деления пополам). Главное в этом деле - иметь острый нож и постоянно смачивать его в уксусной воде.
8. Полученные кусочки разложите на блюдо, сделайте фотографию, после чего принимайтесь за их уплетание :) Приятного аппетита!
Описание вышло очень коротким, чтобы простота и лёгкость были очевидны. Подробности рекомендую уточнить, например, в этом рецепте приготовления суши с хорошими фотографиями и дельными пояснениями.
Теперь перейдём к технике безопасности: Очень распространено заблуждение о том, что в красной рыбе не бывает опасных для человека паразитов. Ссылку об анизакидозе я вам открывать не рекомендую, если будете использовать надёжную рыбу, которую морозили больше 10 дней или правильно засаливали. Есть люди, которые не едят суши по идейным соображениям - не имеют доступа к качественной рыбе, поэтому не хотят рисковать здоровьем ради вкусной еды. Им я рекомендую делать суши из крабовых палочек или речной хорошо прожаренной рыбы (или даже мяса). Получается вкусно и здорово!
Суши, сделанные своими руками - это отличный повод пригласить друзей, прекрасный подарок себе и близким, вкусный и полезный ужин :)
Хорошего вам дня и вкусных выходных!
1 сент. 2009 г.
Хорошая осанка
Часто бывает так: если ребёнка в раннем детстве научили читать и считать, то он верит, что это «получилось само» - он сам собой вырос таким умным. Поэтому через десятилетия такие родители частенько не видят причины отдельно развивать своих собственных детей - ребёнок поздно осваивает базовые навыки, имеет проблемы с учёбой, зубрит вместо общения, потому что не успевает за всеми... А все ещё удивляются, как же у таких умных родителей такое медленное дитя.
Общая формулировка на эту тему звучит так: родители беспокоятся о тех свойствах ребёнка, которые не успели развить в себе, но забывают помочь с тем, что имеют сами.
 Если родителям повезло в своём детстве много бегать по двору, лазать через заборы и по деревьям, играть в футбол на ближайшей площадке, часто ходить плавать на речку и так далее, то они имеют развитое и здоровое тело. И они просто не знают многих бед со здоровьем, потому что почти не болеют.
Если родителям повезло в своём детстве много бегать по двору, лазать через заборы и по деревьям, играть в футбол на ближайшей площадке, часто ходить плавать на речку и так далее, то они имеют развитое и здоровое тело. И они просто не знают многих бед со здоровьем, потому что почти не болеют.И их дети получают немало родительского внимания в тех областях, где родители чувствуют свои слабости (компьютеры, например). Но этим родителям даже в голову не приходит прикладывать усилия для приобщения своих детей к спорту. Ведь они не помнят, чтобы какие-то усилия прикладывались в их детстве - всё вышло как будто само.
Кстати, дети сутулых родителей нередко оказываются очень физически развитыми (несмотря на вроде бы негативный домашний пример). Я думаю, лет в 25 их родители осознали, что почти всё потеряно, что никакими массажами и упражнениями они себе осанку не вернут, спина всегда будет круглой, а здоровье - слабым. И тогда они решают оградить от этих граблей своих детей. Маленький ребёнок не понимает, что в зрелом возрасте будет очень страдать от неправильной осанки, но почти ничего не сможет с этим сделать (просто потому что с возрастом возможности коррекции ощутимо снижаются). А взрослые всё понимают, но почему-то делают для детей мало (это видно по безумному количеству сутулых детей).
За партой надо сидеть симметрично, плечи не должны быть задраны или наклонены - это всё очевидно. И за этим нужно следить учителям в школе, а родителям - дома. На картинке выше предложена конструкция парты, обеспечивающей ребёнку удобную посадку (идеальный вариант - найти школу, в которой хотя бы в начальных классах парты регулируются). Конечно, идеально было бы регулярно делать правильную гимнастику, развивающую и укрепляющую мышцы спины и живота. Если у ребёнка уже есть проблемы с осанкой, то специальные упражнения просто необходимы (обязательно надо посетить специалиста, потому что для различных нарушений нужны разные комплексы).
Осанка - это привычка, её надо формировать осознанно. Но чтобы дать ей шанс закрепиться, нужны мышцы. Плавание и гимнастика - замечательные виды спорта для развития спины. Но если ребёнок всё это не любит - пусть бегает играть в футбол или волейбол, пусть занимается борьбой или теннисом, пусть катается на лыжах или велосипеде, пусть занимается бальными танцами, пусть ему нравится хоть какая-нибудь активная физическая деятельность. Хорошо, если есть родительский пример, тогда ребёнка проще раскачать на что-то такое. Хорошо, если есть спортивные друзья - они любому привьют хорошее здоровье.
Главное: если у вас лично хорошее здоровье, то обратите внимание на своих детей! Они могут не повторить ваш путь, а потом жалеть об этом всю жизнь (и, вообще говоря, укорять своих родителей за бездействие). Рекомендую на эту тему грамотную статью Хорошая осанка: так держать! с сайта газеты «Первое сентября» (в частности, там описаны общеукрепляющие упражнения).
Здоровья вам и вашим детям!