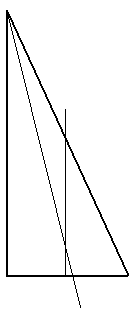
 Сегодня я попробую «доказать» теорему о том, что все прямоугольные треугольники являются равносторонними. Что вообще можно делать с подобными теоремами? Хорошо бы, например, уметь их опровергать. Помните, в разборе парадокса о двух конвертах мы представили ситуацию, которая удовлетворяет условию задачи, но опровергает предположение о том, что вероятности двух конкретных событий равны? Аналогично можно поступить и с данной теоремой - можно предъявить конкретный прямоугольный треугольник со сторонами разного размера (как на рисунке справа). И это полностью опровергнет всю теорему о равенстве сторон любого прямоугольного треугольника. Да и понятно, что слово «доказать» взято в кавычки, потому что хочется лишь создать иллюзию, что доказательство существует и корректно.
Сегодня я попробую «доказать» теорему о том, что все прямоугольные треугольники являются равносторонними. Что вообще можно делать с подобными теоремами? Хорошо бы, например, уметь их опровергать. Помните, в разборе парадокса о двух конвертах мы представили ситуацию, которая удовлетворяет условию задачи, но опровергает предположение о том, что вероятности двух конкретных событий равны? Аналогично можно поступить и с данной теоремой - можно предъявить конкретный прямоугольный треугольник со сторонами разного размера (как на рисунке справа). И это полностью опровергнет всю теорему о равенстве сторон любого прямоугольного треугольника. Да и понятно, что слово «доказать» взято в кавычки, потому что хочется лишь создать иллюзию, что доказательство существует и корректно.Помните, мы недавно разбирали доказательство того, что все лошади одного цвета? Там было неправильное применение метода математической индукции, приводящее к нелепому выводу. И польза такой задачки состоит в появлении дополнительного самоконтроля - теперь, применяя этот метод, человек будет внимательнее, поэтому будет реже обманывать себя по поводу менее очевидных утверждений.
Когда несколько раз проверяешь все пункты доказательства, убеждаясь, что на каждом шаге всё корректно, но итоговый результат очевидно ошибочный, то приходится копаться в себе всё глубже и глубже - а это очень полезно. Почему мы ищем ошибку? Просто из-за того, что хочется понять, как эта простенькая задачка для шестого класса вдруг обводит умного человека вокруг пальца... Ну а если кого-то не обводит, то данное вступление было не для вас :)
 Итак, сначала вспомним пару признаков равенства прямоугольных треугольников, чтобы было на что ссылаться потом:
Итак, сначала вспомним пару признаков равенства прямоугольных треугольников, чтобы было на что ссылаться потом:1) Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
2) Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники тоже равны.
Для краткости я их здесь доказывать не буду. Отмечу только, что первый признак прямо следует из признака равенства треугольников (по двум сторонам и углу между ними), а второй очевиден из теоремы Пифагора - гипотенузой и одним из катетов жёстко задаётся второй катет (обычно его доказывают иначе, но не в этом суть).
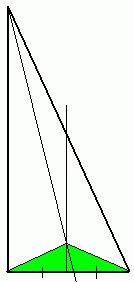 Начнём работать с произвольным прямоугольным треугольником. Возьмём, например, тот, что был на первой картинке. И построим в нём биссектрису из любого острого угла (разделим угол пополам). А из катета, соседнего с другим острым углом, проведём серединный перпендикуляр (перпендикулярную прямую, проходящуюю через его середину). Далее мы построим два отрезка из точки их пересечения - до вершин прямого угла и того острого, который соседствует с данным катетом. На рисунке слева вы можете видеть два зелёных треугольника, равенство которых мы сейчас докажем.
Начнём работать с произвольным прямоугольным треугольником. Возьмём, например, тот, что был на первой картинке. И построим в нём биссектрису из любого острого угла (разделим угол пополам). А из катета, соседнего с другим острым углом, проведём серединный перпендикуляр (перпендикулярную прямую, проходящуюю через его середину). Далее мы построим два отрезка из точки их пересечения - до вершин прямого угла и того острого, который соседствует с данным катетом. На рисунке слева вы можете видеть два зелёных треугольника, равенство которых мы сейчас докажем. Итак, почему же они равны? Это два треугольника, у которых есть один общий катет (значит он у обоих треугольников имеет одну длину). И второй катет - это половина нижнего отрезка, так как мы на нём строили серединный перпендикуляр. Другими словами, два зелёных треугольника равны по первому признаку - у них попарно совпадают длины катетов. Верно? Тогда идём дальше.
Итак, почему же они равны? Это два треугольника, у которых есть один общий катет (значит он у обоих треугольников имеет одну длину). И второй катет - это половина нижнего отрезка, так как мы на нём строили серединный перпендикуляр. Другими словами, два зелёных треугольника равны по первому признаку - у них попарно совпадают длины катетов. Верно? Тогда идём дальше.Из той же точки пересечения биссектрисы и серединного перпендикуляра опустим два перпендикуляра - на гипотенузу и на катет. Получаем ещё два прямоугольных треугольника (рисунок справа). На этот раз мы докажем, что эти голубые треугольники равны.
У них есть общая гипотенуза, поэтому можно попробовать применить второй признак (о равенстве гипотенуз и катетов). Поскольку перпендикуляры опускались из точки, лежащей на биссектрисе, то их длины совпадают по свойству биссектрисы (так как это множество точек, равноудаленных от сторон угла) - данное равенство отмечено одинарными штрихами на чертеже. Получается, что выполнено условие - гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника. Это значит, что голубые треугольники тоже равны.
 Что это нам даёт? Подождите одну секундочку, осталось совсем чуть-чуть!
Что это нам даёт? Подождите одну секундочку, осталось совсем чуть-чуть!Рассмотрим оставшиеся два жёлтых треугольника (на рисунке слева):
Раз зелёные треугольники равны, значит их гипотенузы тоже равны. Но они совпадают с гипотенузами жёлтых треугольников. Это значит, что гипотенузы жёлтых треугольников тоже равны - отметим это на чертеже двойными штрихами.
Ну а раз голубые треугольники равны, то и их катеты равны. Но они совпадают с катетами жёлтых треугольников, поэтому катеты жёлтых треугольников тоже равны (отметим это на чертеже одинарными штрихами).
Выходит, мы опять можем применить второй признак - гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника. Получается, что жёлтые треугольники тоже равны.
 В этот момент уже можно говорить «упс» :)
В этот момент уже можно говорить «упс» :)Если проблема ещё не видна, то предлагаю взглянуть на чертёж справа. На нём отмечены равные стороны жёлтых и голубых треугольников. Хорошо видно, что катет и гипотенуза исходного треугольника состоят из пары одинаковых отрезков. Это значит, что катет и гипотенуза исходного треугольника равны.
Какие это открывает просторы? Огромные! Если один катет равен гипотенузе, то и второй катет тоже равен гипотенузе (по этой же теореме). А это значит, что все прямоугольные треугольники являются равнобедренными - у них равны катеты. А раз оба катета равны гипотенузе, то все прямоугольные треугольники являются равносторонними!
После этого геометрия становится простой и ясной, потому что уж с равносторонними треугольниками мы управимся :)
Повторюсь: я знаю о существовании прямоугольных треугольников с неодинаковыми сторонами, поэтому не надо опровергать данное доказательство словами «доказана глупость, поэтому в доказательстве ошибка». Интересно именно найти эту ошибку :)
Приглашаю обсудить сомнительные моменты доказательства в комментариях (но предлагаю сначала найти своё возражение, а не читать сразу чужие). И очень прошу тех, кто раньше сталкивался с этой задачкой, не рассказывать все секреты, чтобы не лишать остальных читателей удовольствия от самостоятельного разбора. Дело в том, что таких красивых задачек очень мало, поэтому будет очень обидно, если человек, желающий с ней разобраться (и получить от этого себе пользу) не успеет сделать это до того, как кто-то всё объяснит.
Хороших вам выходных!
Подсказка: интересное положение (реальное) одной из точек на чертеже.... )
ОтветитьУдалитьТакую задачу всегда полезно вспомнить, спасибо.
ОтветитьУдалитьНе понял, что означает слово "реальное" в скобках у анонимного комментатора.
Спасибо за задачку. Мне сразу рисунок показался странным, и я нарисовал свой. А дальше уже доказывать ничего не надо было :) А если вспомнить свойства биссектрис, то можно и без рисунка понять, где подвох.
ОтветитьУдалитьА первый аноним видимо и имел ввиду, что надо сделать свой, "реальный", рисунок :)
докажите что вода не круглая
ОтветитьУдалитьСпасибо за задачу. Наконец понял, что срединный перпендикуляр будет пересекать биссектрису не внутри, как на рисунке, а снаружи такого треугольника :-) Да... Мне стыдно, что это не было для меня очевирным. Но я горд, что решил-таки задачу в уме, без собственных чертежей.
ОтветитьУдалитьЗабавная задачка. Только фраза «далее мы построим два отрезка из точки их пересечения» сразу приводит к вопросу «а зачем это они пересекаются?»
ОтветитьУдалить>«далее мы построим два отрезка
ОтветитьУдалить>из точки их пересечения» сразу
>приводит к вопросу «а зачем
>это они пересекаются?»
Это как раз понятно! В прямоугольном треугольнике биссектриса не прямого угла не может быть параллельна срединному перпендикуляру противоположной стороны (кроме вырожденых случаев)
Хм, а если треугольник равносторонний, то биссектриса одновременно является также и высотой - и никакой "точки пересечения" не существует. А коли она является высотой, один из треугольников получается с двумя прямыми углами=)))
ОтветитьУдалитьБиссектриса и срединный перпендикуляр в треугольнике — это не прямые, а лучи. Они не обязаны быть параллельными, чтобы не пересекаться.
ОтветитьУдалитьСогласно свойству биссектрисы, биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.Согласно неравенству треугольника, гипотенуза длиннее любого из катетов. Значит расстояние от точки пересечения биссектрисы и второго катета до вершины прямого угла будет однозначно меньше половины длины этого второго катета. Таким образом, биссектриса и серединный перпендикуляр не могут пересечься внутри прямоугольного треугольника.
ОтветитьУдалитьСпасибо за такую классную задачку! Завидую белой завистью тем людям, которые еще на этапе прочтения Вашего доказательства смогли найти неувязку. Я сразу понял что дело в чертеже, и, нарисовав треугольник с большим катетом внизу и более мелким вверху, понял в чем соль задачи.
ОтветитьУдалитьИ да, нужно еще поправить вот тут:
ОтветитьУдалитьпо двум сторонах -> по двум сторонам
NutipA, спасибо за исправление опечатки!
ОтветитьУдалитьFinrod, в том и дело, что из доказанного прямо следует, что все прямоугольные треугольники являются равносторонними, причём у них все три угла прямые :)
loonyphoenix, не переживайте, на эту задачку в своё время десятки тысяч людей попались :) Говорю же, что она очень хорошая. Жаль только, что рано в комментариях написали о разгадке :(
Но это не фатально, потому что прямоугольный треугольник умеет постоять за себя (смысл этого предложения станет ясен после прочтения следующей заметки :)
если биссектриса и серединный перпендикуляр пересекаются вне треугольника, то доказательство идёт похожим образом, только в конце стороны исходного треугольника образованы не суммой сторон голубого и желтого, а разностью
ОтветитьУдалитьПрикольная задачка :-)
ОтветитьУдалитьЯ сразу не нашел ошибку, потому что давно геометрии никакой не решал. А потом прочитал комментарии и понял, что зря :-( Потому что мог сам разобраться.
Да, зная что доказательство не верно, становится проще. Проходишься по всем утверждениям и проверяешь их истинность. Я, правда, только со второго прохода понял где может быть ошибка.
ОтветитьУдалитьЭто было интересно, спасибо. Хорошо что я не полез в комментарии сразу :)
ОтветитьУдалитьОгромно спасибо всем комментаторам, я вот сразу не догадался, в чем дело)
ОтветитьУдалитьPat, там конфигурация другая будет.
ОтветитьУдалитьСобственно биссектриса пройдёт через середину нижнего катета.
ОтветитьУдалитьИ таких неправильных доказательств, основанных на неточных построениях, можно много придумать.
>Собственно биссектриса пройдёт через середину нижнего катета.
ОтветитьУдалитьНе правда. Это будет только с биссектрисой, проведенной из вершины равностороннего треугольника. А здесь по свойству биссектрисы - она разделит противоположную сторону на отрезки пропорциональные прилежащим сторонам.
"2) Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники тоже равны."
ОтветитьУдалить- это не верное утверждение :) здесь нужно, чтобы еще и угол между катетом и гипотенузой был одинаковым. Доказательство опирается на неверное утверждение
Levon, Вы уверены? ;)
ОтветитьУдалитьВроде бы из теоремы Пифагора следует, что длину одного катета можно определить, зная длину другого катета и длину гипотенузы. А раз они у нас одинаковы для обоих треугольников, то и корни из разности их квадратов тоже равны...
Выходит, что все три стороны одного треугольника соответственно равны трём сторонам другого, из чего следует равенство всех углов :)
Meshok, а почему именно через середину?
Ну, собственно, подвох виден и на чертеже, даже не зная, где на самом деле точка пересечения - ибо перпендикуляры из фальшивой точки явно не равны.
ОтветитьУдалитьЕще в школе в одной умной книжке читал пару таких занятных задач, одна из них, кажется, была именно этой, а вторая - про "тупой угол бывает равен прямому". Жаль, теперь уже найти не могу.
Понял где ошибка когда, для произвольного треугольника сделал теже выкладки и получил его равнобедренным :).
ОтветитьУдалитьсобственно уход в сторону происходит на мой взгляд здесь:
ОтветитьУдалить"Ну а раз голубые треугольники равны, то и их катеты равны. Но они совпадают с катетами жёлтых треугольников, поэтому катеты жёлтых треугольников тоже равны (отметим это на чертеже одинарными штрихами).",
т.е. не те катеты выбраны, ну а дальше что называется "понеслось" ))
HAS, а что не так с выбором катетов? Это же перпендикуляры, опущенные из точки, лежащей на биссектрисе. Поэтому они точно равны.
ОтветитьУдалитьПоглядите на предшествующий чертёж (где только голубые треугольники), там эти же катеты тоже отмечены одинарными штрихами (означающими их равенство). Или Вы не согласны с тем, что голубые треугольники равны?
avialaynen, это дело поправимо. По следующей ссылке Вы можете найти то доказательство равенства прямого и тупого углов - http://xk.kubsu.ru/gr_2.htm
порешал немного в уме и решил нарисовать: сразу пришла решающая идея.
ОтветитьУдалитьвообщем: не верь глазам своим!
задачка прикольная.
Отмечу, что тот факт, что точка пересечения биссектрисы с серединным перпендикуляром находится вне треугольника вовсе не оп;ровергает «доказательство»:
ОтветитьУдалитьhttp://i080.radikal.ru/0909/59/e68e30e9d0c4.jpg
Точно так же доказываем равенство AB1=AC1=x (как перпендикуляров с биссектрисы), а BB1=CC1=y (из равенства по гипотенузе и катету жёлтых треугольничков).
И далее опять получим равенство гипотенузы катету, только уже не как сумму отрезков (x+y), а как их разность (x-y).
На самом деле, дело в том, что перпендикуляры из точки D (пересечения биссектрисы и серединного перпендикуляра) попадут на продолжение катета, но на саму гипотенузу (а не на продолжение), поэтому получим AC=x+y, а AB=x-y и никакого противоречия не получим.
Илья Весенний, как вам задачка из хабравского «топика зла»? http://habrahabr.ru/blogs/zadachki/70573/
Мне лично, с её неожиданным решением, очень понравилась.
А вот реакция хабра-сообщества очень расстроила. Надеялся, что там более адекватные и широко мыслящие люди.
Ответ просто знал, но всё равно спасибо, что напомнили 8)
ОтветитьУдалитьLisandreL, Вы только что рассказали всю cледующую заметку. Сознавайтесь, откуда знали? Где учились? :)
ОтветитьУдалитьА топик зла мне оказался полезным - я придумал другую задачку, глядя на эту. И она мне нравится :)
Отличная задача. После 5ти минут втыкания и недоумения, приходишь к очевидному - они не будут пересекаться внутри треугольника ;)
ОтветитьУдалитьглядя на рисунок,спустя минуту,понимаешь,что точка пересечения биссектрисы с катетом нижним не может быть правее,чем точка пересечения серединного перпендикуляра с этим катетом!
ОтветитьУдалитьХы. Все-таки не даром преподаватели время со мною тратили :)
ОтветитьУдалитьФраза "Нарисовать хороший чертеж - решить половину задачи" вылезла откуда-то там из головы и заставила нарисовать все самому :)
ps. (не по теме) вспоминая школьные годы, помнится, на олимпиаде по математике я долго возился с задачей (а основа там была - прямоугольный треугольник), но никак не мог найти один угол (..угол между отраженным лучом, делящего чего-то там пополам, и еще чего-то:). В результате построит на двойном тетрадном листе большой чертеж, измерил этот угол транспортиром и написал это в ответ (с указанием ГОСТа транспортира). Как оказалось, я был чуть ли не единственным кто дал, хоть какой-либо ответ и мне зачли половину баллов задачи :)
А разве биссектриса не должна закнчиться там, где начинается срединный перпендикуляр? Тогда и трегольников не было бы в начале.
ОтветитьУдалитьDi, биссектриса угла - это луч, выходящий из вершины угла и делящий его пополам. Он вообще ничего не знает о других отрезках, поэтому не прерывается, уперевшись в противоположную сторону треугольника или какой-либо другой отрезок :)
ОтветитьУдалитьЯ думаю, Di имел(а) в виду, что биссектриса пройдет через середину противолежащего катета, но это, очевидно, не так.
ОтветитьУдалитьarxz, спасибо за уточнение! Теперь я понял, что хотел сказать Di.
ОтветитьУдалитьБог с Вами, вы неверно отметили равные стороны у желтых треугольников!
ОтветитьУдалитьУважаемый аноним, Вы можете указать на ошибку в рассуждении, на основании которого стороны жёлтого треугольника так отмечены? Если да, то Ваше заявление имеет смысл. Если нет, то это просто слова.
ОтветитьУдалитьОшибка в предположении "Хорошо видно, что катет и гипотенуза исходного треугольника состоят из пары одинаковых отрезков."
ОтветитьУдалитьЕсли до этого все логические рассуждения были вполне корректны, то вывод про "...состоят из пары одинаковых отрезков..." сделан на основании только построения и бездоказателен.
Из попарного равенства отрезков, лежащих на двух прямых следует лишь равенство сумм их длин. Но вовсе не следует, что отрезки, образованные начальными точками первых отрезков и конечными точками вторых, будут также равны между собой. На это ещё влияет и взаимное расположение отрезков на прямой.
Именно про особенности этого взаимного расположения автор задачи предусмотрительно умолчал, нарисовав схему построения таким образом, чтобы читатели были введены в заблуждение.
Как человек доверчивый, не стал задумываться о месте пересечения биссектрисы и срединного перпендикуляра, зациклившись на логике) В результате пришлось перечитывать, и лишь на последнем рисунке увидел вопиющее (спасибо не могущей соврать геометрии) неравенство углов по обе стороны "биссектрисы")) После этого, как вы понимаете, все пошло быстро, на всякий запасный построил график)))
ОтветитьУдалитьТаким же методом можно доказать, что любой произвольный треугольник равносторонний.
ОтветитьУдалитьВсякие подобные "доказательства" можно найти, например в Дубнов Я.С. "Ошибки в геометрических доказательствах",Москва, "Наука" 1969г. серия "Популярные лекции по математике" выпуск 11 (книжка в сети есть). Новое - давно забытое старое (уже в 1969 году четвертое издание было) :) - все это хорошо известный "фольклор":)
ОтветитьУдалитьУважаемый аноним, спасибо, что напомнили ещё одну хорошую книгу.
ОтветитьУдалитьДавайте продолжим рассуждения... Из теоремы Пифагора видно, что нижний катет будет равен нулю, а значит все доказательство справедливо для вырожденных треугольников. Таким образом приведенное выше рассуждение говорит о том, что если один из катетов равен нулю, то гипотенуза будет равна второму катету, а противолежащий ему угол будет прямым. И никакого противоречия!
ОтветитьУдалитьPS:
Ну и предлагаю поразмышлять насколько справедливо называть вырожденный треугольник треугольником.
Из википедии: треугольник это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Следовательно вырожденный треугольник нельзя называть треугольником. К тому же второй признак равенства треугольников (по двум углам и стороне между ними) несправедлив для вырожденных треугольников - пример : сторона равна нулю, а углы прямые.
С уважением Андрей!