Интересное в июне

Добрый день!

Традиционно предлагаю новым читателям ознакомиться с некоторыми материалами из архива блога - за июнь прошлого года. В тот месяц мы говорили о взаимодействии людей и образовании:

1. В заметке «Об изменчивости» речь шла о том, что людям свойственно корректировать свои воспоминания, не отдавая в этом отчёта даже себе. В частности, так получается из-за того, что обычно говорят о какой-то конкретной личности, а не о личности в данный конкретный момент. Но люди-то меняются! Одного часа может не пройти с момента произнесения какой-то фразы, а человек уже поменяется - станет другим, не помнящим, что он что-то там говорил. Этому трудно противостоять, но надо хотя бы понимать.

2. Ещё в июне можно было коротко поговорить о ЕГЭ 2009. Ситуация стала более предсказуемой, проявились некоторые плюсы (например, дети сильнее защищены от самодурства отдельных учителей), но непрозрачные ухищрения с растяжениями шкал удивляют и огорчают. Через полгода можно будет сравнить эти ощущения с результатами ЕГЭ 2010 года.

3. А в заметке «Нечёткие формулировки» мы рассматривали пару задачек с очень короткими, но не ясными условиями. Проблема в том, что такие задачи не могут быть решены, например, компьютером. Но десятки тысяч людей понимают их с одного взгляда, умея отличать верное понимание от ошибочного. Более того, хорошая задачка обладает следующим свойством: решив её, не приходится спрашивать чьего-то подтверждения, потому что правильное решение само выглядит правильным.

Хорошего вам дня!

Запись о заметках прошлых месяцев стала традиционной, поэтому перечислю предыдущие выпуски: интересное в мае, интересное в апреле, интересное в марте, в феврале, январе 2009 года, декабре, ноябре, октябре, сентябре, августе, июле и июне, интересное в первые три месяца жизни блога.

Плотность распределения

Добрый день.

Вчера мы считали вероятности для частного случая задачи о двух конвертах, а сегодня будем разбираться, где там была ошибка и почему с «очевидными» решениями надо быть очень аккуратным.

Если вы ещё не прочитали прошлую заметку с ошибкой, то дальнейшее чтение этой записи особой пользы не принесёт. Опыт показывает, что особенно хорошо удаётся понять те грабли, на которые только что наступил. Поэтому я рекомендую сначала прочитать вчерашнее рассуждение, чтобы интуиция подтвердила, что «так всё и есть» (или разум остановил, потому что «так не бывает»).

Действовать сегодня будем так:
1. Поставим эксперимент, чтобы убедиться в наличии ошибки.
2. Рассмотрим наглядное и интуитивно понятное объяснение. Так будет легче почувствовать, что именно сделано «не так».
3. Решим задачу честно, а не как вчера.

Одна из главных тонкостей рассматриваемого частного случая - непрерывность интервала, на котором мы работаем. Если бы было известно, что в конвертах могут быть только целые значения, то мы бы не допустили ошибки, потому что отдельно рассмотрели бы случаи чётной и нечётной сумм в конвертах: если сумма нечётная, то заведомо надо менять конверт, так как в нём меньшее из двух значений. Но в непрерывном случае этой проблемы нет, поэтому ничего не мешало ошибиться.

1. Как и договаривались, сначала поставим эксперимент, чтобы снять многие сомнения. Если верить статистике, большинство подписчиков используют Google Reader. Это значит, что как минимум браузер, способный выполнять Javascript, есть почти у всех. Задача у нас простая, поэтому и эксперимент ставится в несколько строчек:

<script type="text/javascript">
  m = 10;  // min value
  n = 100; // max value
  var q = [0, 0]; // init quantities
  for(i=0;i<10000;i++) { // nb experiments
    r = (Math.random()*(n-m+1))+m; // random value from 10 to 100
    var v = [r, 2*r];  // generate pair of envelopes
    c = (Math.random() > 0.5) ? 0 : 1; // random envelope
    chosen = v[c]; // value in chosen envelope
    if ( (chosen >= 20) && (chosen <= 100) ) // interesting
      q[c]++; // calc quantities
  } // for
  document.write('Quantities of envelopes on [20..100]: '+
    q[0]+', '+q[1]+', ratio: '+q[0]/q[1]); // print anwer
</script>

Что получается? Как минимум, результат заметно отличается от «доказанного» вчера. Для случаев, когда в вытянутом конверте сумма лежит в интервале от 20 до 100, мы посчитали количества ситуаций 'конверт оказался меньшим из двух' и 'конверт оказался большим из двух'. Выяснилось, что первое число примерно в два раза больше, чем второе. Но вчера-то мы пришли к выводу, что эти числа должны быть примерно равны!

2. Теперь давайте подключим воображение. Вчера я предложил неправильную иллюстрацию, чтобы возникло сомнение. На картинке справа мы видим голубой прямоугольник - он соответствует графику плотности случайной величины, равномерно распределённой от 10 до 100 (значение в меньшем конверте).

А жёлтый прямоугольник соответствует графику плотности случайной величины, равномерно распределённой от 20 до 200. Площади под графиками должны быть одинаковыми, а жёлтый прямоугольник в два раза шире, поэтому он в два раза ниже синего. Там, где наши прямоугольники пересекаются, цвета для наглядности «смешиваются» - получаем зелёный цвет.

Чтобы было проще представить, передвинем часть синего прямоугольника вверх - так мы избежим пересечения. Теперь очень хорошо видно, что для любого числа, попавшего в интервал от 20 до 100, вероятность того, что оно является меньшим в своей паре (синим), в два раза превосходит вероятность того, что оно большее в своей паре чисел (жёлтое).

Такая визуализация очень полезна, так как подобные образы хорошо помогают интуиции свыкнуться с не очень естественными вывихами реального мира. Да, теперь чётко видно, что вероятности событий '2X во втором конверте' и 'X/2 во втором конверте' не могут быть равны. Но это только вспомогательная иллюстрация, а не решение.

3. А теперь решим задачу честно.
Введём два равновероятных события H1 и H2: это вытягивание первого и второго конверта. И события A - попадание случайной величины X в интервал от 20 до 100.

То есть, имеем следующее:
P(H1)=P(H2)=1/2,
A = {20 <= X <= 100}.

Тогда рассчитаем условные вероятности (P(A|B) - это вероятность того, что событие A произошло, если уже произошло событие B):
P(A|H1) = P(A∩H1) / P(H1) = 8/9,
P(A|H2) = P(A∩H2) / P(H2) = 4/9.

Если это не выглядит понятно, то предлагаю ознакомиться с прозрачным комментарием AAbrosov. Он разбил интервал на 19 равных областей длины 10 (от 10 до 20, от 20 до 30, ... от 190 до 200). Первый конверт одинаково часто попадает в первые 9 интервалов, а второй - одинаково часто попадает в последние 18 интервалов. Остаётся посчитать, с какой вероятностью каждый из конвертов попадёт в интересную нам область от 20 до 100. Первый конверт это делает в 8 случаях из 9 (все интервалы, кроме [10..20]). А второй конверт это делает в 8 случаях из 18 (все интервалы, кроме последних 10 [100..110], [110..120], ... , [190..200]). Так мы получили те же условные вероятности, но чуть длиннее и нагляднее.

А что нам надо найти? Нам нужно P(H1|A) - вероятность того, что мы вытянули первый конверт при том, что мы уже попали в интересный нам интервал (от 20 до 100).

Посчитать это нам поможет теорема Байеса:
P(H1|A) = (P(H1)P(A|H1)) / (P(H1)P(A|H1) + P(H2)P(A|H2)) = (4/9) / (4/9 + 2/9) = 4/6 = 2/3.

Так мы вычислили, что если в вытянутом конверте оказалось от 20 до 100 денег, то с вероятностью 2/3 этот конверт является меньшим в своей паре. Раньше мы имели иллюзию, что эта вероятность 50%, поэтому ожидали, что смена конверта принесёт +25% к текущей сумме в среднем (так как (2X+X/2)/2 = 5X/4). Но теперь мы понимаем, что 2X во втором конверте будет с ещё большей вероятностью.

Поэтому правильные вычисления выглядят так: (2*2X + 1*X/2)/3 = 3X/2. Другими словами, замена конверта позволит увеличить сумму в полтора раза (в среднем). Поэтому его тем более надо менять.

Получается, что полный ответ к данному частному случаю задачи о двух конвертах звучит так:
- Если вытянутое число больше 100, то менять конверт не следует, так как это гарантированно приведёт к уменьшению выигрыша,
- Если вытянутое число меньше 20, то обязательно надо сменить конверт, так как это гарантирует увеличение выигрыша,
- В остальных случаях тоже следует сменить конверт, так как вероятность удвоения суммы в два раза больше вероятности её сокращения, да ещё и возможный выигрыш при замене больше возможного проигрыша.

Будьте осторожны с рассуждениями о вероятностях. Часто так бывает, что всё выглядит правильно и очевидно, но оказывается совершенно неверным. И чем рассуждение яснее и очевиднее, тем сильнее заблуждение :)

Хороших вам выходных!

Считаем вероятности

Добрый день, дорогие читатели!

Продолжаем делать добрые дела вместе с вами:
- в августе прошлого года вы исправили статью википедии, содержавшую явный бред по поводу задачи о двух конвертах,
- на этой неделе, разбираясь с сектантами на острове Беззеркалья, вы исправили другую статью википедии. И это тоже добавило адекватности всемирной энциклопедии (жаль, что ту статью пока никто не перевёл на русский язык).

Но можно ли на этом остановиться? Увы, плюсы открытой википедии часто становятся её минусами: любой человек, не разбирающийся в предмете, может внести в неё что угодно. И это делается не со зла, а из-за искренней убеждённости в своей правоте (логические парадоксы умеют перетягивать в неправильную сторону). А понимающим людям часто даже не приходит в голову читать подобные статьи, поэтому ошибки такого типа копятся (а потом тиражируются, например, журналистами).

В наш век быстрого распространения бреда информации есть два варианта: уметь фильтровать откровенную ложь или слепо следовать за красивыми словами тех, кто даже не понимает своей собственной позиции.

На мой взгляд, разбор логических, геометрических и вероятностных задач очень полезен. Дело в том, что человек, разобравшийся с подобным решением, уже не так легко верит на слово красивым высказываниям о вероятностях и математических ожиданиях, не покупается на цветные графики и чертежи. А это несколько ограничивает влияние манипуляторов на действия большинства.

Поэтому сегодня я предлагаю вернуться к парадоксу двух конвертов, чтобы разобрать один частный случай. Я уверен, что многие из вас сами могли найти, понять и исправить ту ошибку. Но уже несколько месяцев она висит в статье википедии, поэтому я предлагаю в неё вникнуть чуть подробнее.

Коротко напомню постановку задачи: есть два конверта, в одном из которых находится сумма вдвое большая, чем в другом. Игрок выбирает один конверт, пересчитывает в нём деньги, а после этого решает, оставить его себе, или взять другой.

Интуиция подсказывает, что если в первом вытянутом конверте находится X денег, то во втором с раными вероятностями будет X/2 и 2X. В прошлом году мы разобрались с этим заблуждением. Но до сих пор поступают комментарии от людей, которые не очень уверенно умеют рассчитывать вероятности сумм во втором конверте для частных случаев.

Да и в упомянутой статье википедии содержатся неверные выкладки. Цитата: «Например, если предположить, что сумма в меньшем конверте равномерно распределена между 10 руб. и 100 руб., очевидно такое:
* Если выпало 15 руб., в другом конверте определённо 30 руб. (7,5 быть не может). Поэтому требуется брать другой конверт.
* Если выпало 25 руб., в другом может быть как 12,5 руб., так и 50 руб., но вероятность второго больше — желательно брать другой конверт.
* Если выпало 90 руб., в другом может быть как 45 руб., так и 180 руб., при этом больше вероятность первого — лучше не брать другой конверт.
* Если выпало 100 руб., в другом конверте определённо 50 рублей — ни в коем случае не брать другой конверт».

Вам тоже кажется, что последние три пункта как минимум странные? И то, что они предваряются словами, «очевидно такое», никак не улучшает ситуации.

Давайте честно рассчитаем вероятности! В меньшем конверте находится случайное число от 10 до 100, поэтому в большем - от 20 до 200. Это значит, что вытянув конверт, мы можем получить какое-то число от 10 до 200. Давайте разделим этот интервал на три части:
1) 10 <= X < 20,
2) 20 <= X <= 100,
3) 100 < X <= 200.

Чем хороши первый и третий диапазоны? Тем, что попав в них (не важно с какой вероятностью), мы точно знаем, сумма в нашем конверте X является большей из двух сумм в конвертах или меньшей. Это значит, что если X<20 или если X>100, то мы на 100% уверены, что делать.

Осталось разобраться со средним диапазоном. Давайте поймём, как формируются конверты:
- кто-то умеет генерировать случайные величины Y от 10 до 100, равномерно распределяя числа в этом диапазоне,
- кто-то другой берёт эти числа, чтобы сформировать пару для конверта (Y, 2Y) - это наши равновероятные элементарные исходы,
- мы (игрок) вытягиваем число X, открыв случайный из этих двух конвертов.

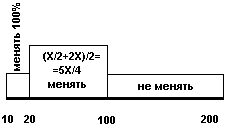И как же было получено это число X? Очень просто - оно оказалось большим или меньшим в сгенерированной паре (Y, 2Y). Другими словами, нам досталась одна из пар (X, 2X) или (X/2, X). А мы вытянули из неё число X.

Но мы же знаем, что меньшее число в этих парах - случайная величина, имеющая равномерное распределение на диапазоне от 10 до 100. Это означает, что все пары (Y, 2Y) появляются с равными вероятностями. И из этого следует, что вероятности генерации пар (X, 2X) и (X/2, X) одинаковы, так? Поэтому, если уж нам досталось число X от 20 до 100, то вероятности того, что во втором конверте будет 2X или X/2 равны, верно?

Поэтому «правильный» вывод состоит в следующем:
- Если вытянутое число больше 100, то менять конверт не следует, так как это гарантированно приведёт к уменьшению выигрыша,
- Если вытянутое число меньше 20, то обязательно надо сменить конверт, так как это гарантирует увеличение выигрыша,
- В остальных случаях тоже стоит сменить конверт, так как вероятность удвоения суммы равна вероятности её сокращения в два раза, но возможный выигрыш при замене больше возможного проигрыша.

Всё это очень просто и для дискретного случая (когда в конвертах могут быть только целые числа, например). Только тогда придётся вникать в чётность (так как нечётный X однозначно указывает на то, что следует поменять конверт), а это сделает решение чуть более громоздким.

Хорошего вам дня и интересного чтения энциклопедий!

P.S.
кстати, кто заметил ошибку в рассуждениях выше? ;)

Дополнение: пояснения даны в следующей заметке.

Три решения

Сегодня в нашей рубрике «Три чего-нибудь» будет три ответа на вопросы, часто задаваемые начинающими пользователями ПК. Я немножко утомился разрешать их индивидуально, поэтому сейчас попробую сделать это оптом. Надеюсь, вам эта заметка поможет сэкономить время - можно будет просто сразу показать её вопрошающим :)

Итак, вопросы:

1. Как прочитать «кракозябру» на mail.ru?
Проблема обычно выглядит так: с какой-нибудь зарубежной почтовой системы приходит письмо на русском языке, но веб-интерфейс mail.ru отображает его в странном виде. Например, таким образом: «Б з Ц М щ я ш Ю Д И ж Д». Что с этим делать? Как расшифровать текст, отображающийся в неправильной кодировке?

В простом случае достаточно показать автору вопроса декодер Лебедева. Но должен предупредить, наш сегодняшний рецепт для очень странных ошибок с кодировками. Если декодер не справляется, то есть ещё один ход, который мне неоднократно позволял помочь с прочтением важных писем.

Достаточно нажать в веб-интерфейсе на «дискетку», чтобы появился диалог сохранения письма. В скачанном файле будет первозданная информация о кодировках, потому что несовершенные системы декодирования её ещё не повредили. Поэтому нормальные почтовые программы почти всегда могут корректно отобразить такое скачанное письмо. Для большинства пользователей это означает, что надо просто «запустить» полученный .eml-файл - дальше почтовая программа сама покажет текст присланного письма.

2. Как сохранить gif-файл в mspaint (microsoft paint), чтобы цвета не поехали? И как при этом избежать ряби?

Да, есть люди, которые делают простенькие изменения картинок в этом ужасном редакторе. И если я скажу, что так жить нельзя, то им это не поможет. Потому что у них нет никаких внутренних сил для освоения любого другого графического редактора.

Не будем сейчас обсуждать вопрос потакания слабостям, а найдём работающее решение. Итак, справа мы имеем три картинки:
- исходная,
- нормально сохранённая в GIF,
- сохранённая в GIF через MSPaint.

Зачем вообще нужно сохранять в GIF? Ответ простой: «требование заказчика». Но нельзя же этому заказчику показывать нижнее изображение... Средняя картинка вполне бы всех устроила (дефекты на ней неизбежны из-за обилия разных цветов), но узоры нижнего изображения кого угодно выведут из себя. Добавлю, что для получения таких неприемлемых эффектов можно воспользоваться картинкой с куда меньшим количеством цветов.

Что же делать?

Я предлагаю следующий путь:
1. Зайти на страницу загрузки IrfanView.
2. Скачать и установить эту очень компактную и быструю программу.
3. Для сохранения изображений после их редактирования в paint'е, копировать их целиком в буфер обмена, затем вставлять в IrfanView, а уже из него сохранять в формате GIF. Да, сохранять стало чуть труднее. Но это позволяет показывать результат хоть кому-нибудь :)

Кстати, IrfanView ещё имеет очень ценный плагин JPG_TRANSFORM, позволяющий выполнять JPG lossless rotation. Суть вкратце: любая операция сохранения файла в формат JPG приводит к понижению качества. Поэтому при повороте своих фотографий большинство людей ухудшают картинку. Зачем покупать дорогой фотоаппарат, если потом результат его работы будет перечёркнут неумелым поворотом? Но есть способ избежать этого - проводить честный пересчёт одного JPG-файла в повёрнутый на 90 градусов. Для понимания этого механизма надо знать, как устроен формат JPG. Но для его использования нужно всего лишь скачать программу, которая это умеет.

Это особенно актуально при работе с очень сильно сжатыми изображениями (на которых дефекты компрессии уже хорошо видны). Их поворот с сохранением качества приводит к увеличению размера файла в несколько раз. Если такое распухание недопустимо, то приходится ещё сильнее портить изображение, что тоже может быть запрещено. А lossless rotation легко спасает в этой ситуации.

И последний на сегодня вопрос:
3. Где скачать acrobat reader? (или что-то аналогичное)
Если на вопрошающих грубо не рявкать, то они будут часто спрашивать то, что вполне могут узнать сами. Но зачем портить отношения с вообще-то неплохими людьми? Они всего лишь не имеют острой необходимости освоить компьютер, не имеют к нему интереса или просто боятся.

Есть же простой ответ, который одновременно решает их «проблему» и мягко намекает на то, что она не такая уж сложная. В данном случае, можно было ответить коротко и метко:
http://lmgtfy.com/?q=adobe+reader - откроется строка поисковой машины, в неё автоматически (javascript) будет введён заданный вами текст, после чего кнопка «поиск» перебросит пользователя на результаты. Как правило, если вопрос простой, то и ответ на него будет на первом месте.

А какие ответы вам приходилось давать последнее время?

Удачи вам и вашим пользователям :)

Индукция на острове

В математике всё время так:
или непонятно зачем,
или непонятно как.

Продолжим разбираться со вчерашней задачкой об острове без зеркал. Сначала коротко и сухо вспомним условие:

1. На острове 888 кареглазых и 111 голубоглазых сектантов. Они легко могут видеть друг друга и знают, что людей с другим цветом глаз на острове не может быть. Но каждый из них не знает цвет своих глаз.

2. Все островитяне очень умные, поэтому они догадаются до всего, до чего только можно догадаться. По этой причине они изначально не знают количество голубоглазых и кареглазых на острове (иначе бы они мгновенно вычислили свой цвет глаз).

3. Житель острова, узнавший цвет своих глаз, дожидается ближайшего парома (которые приходят в 17 часов каждый день), чтобы уехать навсегда.

4. Однажды на остров приезжает турист, чтобы пообщаться со всеми островитянами и насладиться красотой острова. Вопреки всем запретам на обсуждения цвета глаз, он во всеуслышание сообщает истинное утверждение, что среди островитян есть хотя бы один голубоглазый.

Вопрос: как поменяется жизнь на острове после отъезда разговорчивого туриста?

Сейчас я должен остановиться на минутку, чтобы предупредить: ниже будут предложены два «очевидно правильных» решения. Я думаю, что гораздо интереснее придумать их самостоятельно. Тогда потом будет дополнительный стимул, чтобы найти «виноватого» :)



Если вы уверены, что уже достаточно подумали, то приступим к разбору:

Первое решение:

Каждый житель острова видел 110 или 111 голубоглазых. Это означает, что каждый сектант знал, что на острове есть хотя бы один голубоглазый. Поэтому слова туриста ничего не меняют - островитяне как жили на острове раньше, так и дальше будут жить.

Второе решение:

Давайте решим эту задачу методом математической индукции. База индукции простая - пусть на острове есть один голубоглазый и много кареглазых сектантов. Получив подсказку от туриста, голубоглазый всё понимает: раз он видит вокруг только кареглазых, а хотя бы один голубоглазый на острове есть, то это именно он. Поэтому он - единственный голубоглазый - уплывёт с острова на первом же пароме.

Кстати, давайте поймём, что будет на следующий день: все кареглазые заметили, что голубоглазый, услышав слова туриста, неожиданно сорвался и уехал. Это означает, что голубоглазый не увидел вокруг себя других голубоглазых. Так все оставшиеся жители острова понимают, что они все кареглазые. Вывод - на второй день они тоже уплывут на пароме. И остров опустеет.

Что же, с базой индукции мы разобрались. Давайте сделаем шаг. Сразу предупрежу, что рассуждение будет достаточно абстрактным, поэтому предлагаю сначала понять более простую ситуацию (первый шаг).

Пусть на острове есть двое голубоглазых и много кареглазых. Как только турист сделал своё заявление, каждый голубоглазый думает: «Я вижу ровно одного голубоглазого. Если он уплывёт сегодня на пароме, значит я кареглазый. А если не уедет, значит он видит другого голубоглазого - меня. Поэтому мне придётся уехать завтра». Другими словами, завтра ему уезжать придётся в любом случае.

Теперь сделаем этот шаг строго. Предположение индукции: если на острове есть N голубоглазых и больше N кареглазых сектантов, то на N-ный день все голубоглазые уедут. А все кареглазые уедут на N+1-ый день

Доказательство: пусть на острове находятся N+1 голубоглазых и больше N+1 кареглазых.
Тогда каждый голубоглазый видит ровно N голубоглазых. И он понимает, что если цвет его глаз не голубой, то они все уедут на N-ный день (по предположению индукции). А раз они на N-ный день не уезжают, то это означает, что у него голубые глаза. Поэтому он должен будет уплыть на N+1-ый день.

Чувствуете проблему? У нас есть два вроде бы правильных решения, приводящих к противоположным ответам. Можно ли теперь пользоваться математической логикой? ;)

Но я уверен, с этим мы скоро окончательно разберёмся в комментариях. Кстати, заранее предупрежу, что в обсуждении предыдущей заметки есть очень точные замечания, поэтому я не рекомендую их читать, если есть желание понять тонкость своими силами. Это того стоит!

А если вы ещё не знаете, что все лошади на планете имеют лиловый цвет, то, возможно, будет полезно разобраться с «доказательством этого факта» - оно является в каком-то смысле базовым для понимания задачи о туристах на острове. Я имею в виду, что есть смысл заранее знать о некоторых ловушках, в которые можно попасть, пользуясь методом математической индукции :)

Хорошего вам окончания недели!

Остров Беззеркалья

Добрый день, дорогие читатели.

Сегодня я предлагаю погрузиться в интересную математическую проблему, выталкивающую пытливые умы к непростому философскому вопросу. Но сначала давайте вспомним, что одна из важнейших функций науки - предсказание. Соответственно, хорошая научная теория способна с высокой точностью предсказывать результаты многих экспериментов. А плохая теория часто ошибается, поэтому её перестают рассматривать.

Каждому ясно, что в физике, химии или биологии эксперименты проводятся постоянно. Но можем ли мы ставить эксперимент в математике? Конечно, можем! В своей голове. Или в компьютере :)

Ниже будет текст задачи, а в следующей заметке два её «очевидно правильных» решения. Тонкость в том, что эти решения приводят к противоположным ответам. И остаётся только развести руками: ошибка явно есть, но где? Или в методе математической индукции, или в математической логике, или в математике вообще. И как тогда можно пользоваться этим инструментом, если он способен предсказать два противоположных исхода?!

Что-то похожее было, когда мы разбирали доказательство того «факта», что все стороны произвольного треугольника равны. Кто-то смог обнаружить ошибку в том «доказательстве», но её удалось быстренько закрыть. Конечно, потом мы окончательно разобрались с хитрой геометрической задачкой. Но в тот раз мы точно знали, что бывают треугольники со сторонами разной длины. Другими словами, было ясно, куда копать. А в сегодняшней задачке, я надеюсь, эта ясность придёт далеко не сразу.

Итак, вводная:
На острове Беззеркалья счастливо живут 888 кареглазых и 111 голубоглазых сектантов. Религия им всем предписывает покинуть остров в течение суток, если они узнают цвет своих глаз. Поэтому на острове нет зеркал и никто не ведёт бесед о глазах. И каждый день в 17 часов на остров прибывает паром, увозящий несчастных, которые каким-то образом случайно узнали цвет своих глаз, на другой остров «Ад» (там живут сектанты, знающие цвет своих глаз).

Уезжать на другой остров никто не хочет (наверное, название не нравится). Но если вдруг узнал цвет своих глаз, то вера обязывает это сделать. При этом никто не хитрит: если до чего-то можно догадаться, то они догадываются. Все жители острова очень умные!

Что происходит дальше? На наш бедный остров обрушивается всепроникающая демократия. Хорошо ещё, что происходит это в не очень большом масштабе: приезжает всего один американский турист. Много это или мало? Скоро узнаем!

Американский турист был подробно проинструктирован представителями ЮНЕСКО. Ему объяснили, что нельзя никак информировать островитян о цвете глаз, потому что для мировой культуры крайне важно сохранить эту очень умную, но весьма странную популяцию. Её ведь очень трудно восстанавливать! Почти все люди нашей планеты знают цвет своих глаз, поэтому не могут стать новыми жителями острова Беззеркалья.

Экскурсии прошли очень хорошо и интересно: островитяне показали американцу свои театры, музеи, библиотеки, метро (единственная в мире действующая сеть станций метро, состоящая всего из одной станции) и знаменитые статуи с закрытыми глазами. Поскольку жителей на острове мало, то американец смог увидеть каждого (и все об этом знают). Прощаясь, растроганный турист сказал: «Спасибо вам большое за тёплый и дружественный приём! Особенно приятно было в этом дивном месте встретить человека с такими же голубыми глазами, как у меня.»

На этом условие задачи заканчивается, а начинается вопрос: как поменяется жизнь на острове после отъезда разговорчивого туриста?

Пояснения:

0. Жители острова легко могут видеть друг друга. Они вообще общительные ребята - никто по пещерам не прячется. И солнцезащитными очками глаза друг от друга они тоже не прячут :)

1. Раз уж выше был упомянут метод математической индукции, то в следующей заметке будет предложено основанное на нём рассуждение. Но я думаю, что гораздо интереснее придумать его своими силами. Чтобы попытаться понять, есть ли в нём ошибка. И если есть, то где :)

2. Это не очень простая задача. Но для её понимания не надо иметь специальных знаний. Достаточно сосредоточиться. У меня ушло несколько дней на размышления, но неожиданное озарение щедро вознаграждает. Желаю всем пройти таким путём! Это того стоит.

3. Если вам знакома данная задача, то, пожалуйста, не мешайте другим читателям самостоятельно продвигаться в её понимании. Пожалуйста, не надо делать «прозрачных намёков», отбивающих интерес!

Хорошего вам дня и интересных мыслей!

Извиняюсь за тавтологию (тавтологию)

Вторник, второе августа, время - десять без десяти
Лето в поре, однако сказать, что жарко, никак нельзя. Не жарко.
(c) Михаил Щербаков

Добрый день! Прошу меня извинить за некоторое количество повторов в следующем абзаце ;)

У пишущих и создающих тексты (наборы слов) авторов или людей, имеющих склонность или пристрастие к написанию и генерации текстовой или устной информации и данных, а также у говорящих вслух ораторов порой иногда возникает или может возникнуть позыв и желание высказаться, воскликнув: «Извиняюсь за тавтологию!»

Что это значит? Человек уже чувствует ненужность повтора в своём тексте, но зачем-то его сохраняет! Да ещё и намекает читателю, что он сам прекрасно видел тавтологию, понимает, что она тут излишня... и ничего не меняет. О чём это говорит?

Мы с вами понимаем, что иногда повторы вполне уместны и за них не надо извиняться: «Вот на берег вышли гости, Царь Салтан зовёт их в гости» - Александр Сергеевич после этой строчки не просит у читателя прощения за повтор слова «гости»! И обилие амплификаций в эпиграфе радует ухо. А если мы говорим «согласен целиком и полностью» или «на сегодняшний день», то это вполне грамотно, хоть и избыточно. В русском языке уже есть устойчивые выражения, содержащие повторы:
- «окружен со всех сторон»,
- «видел своими глазами»,
- «жизнь прожить – не поле перейти»
и так далее. Зачем после каждого из них говорить о «тавтологии»?

Если же мы вдруг обсуждаем «чёрные чернила», например, то здесь сомневаться вообще излишне, ведь бывают чернила других цветов. Эти однокоренные слова имеют очень разные смыслы, поэтому их соседство допустимо. Отдельно отмечать такие словосочетания своими извинениями - пустое дело.

Другой пример: «Для хорошего контакта мы зачистили контакты». Мысль нормально изложена. Если у автора нет желания сформулировать это же без повтора слова (потому что от этого вырастет объём, например), то тем более не стоит тратить место на извинения за тавтологию.

Ещё тавтологии часто можно встретить в научных и технических материалах - и это правильно. В таких текстах лучше избежать путаницы в терминах, чем напихать сбивающих с толку синонимов.

Но есть неграмотные и неосмысленные повторы:
- «спросить вопрос»,
- «изобразить образ»,
- «наиболее оптимальное решение»,
- «приблизиться ближе»
и так далее (включив телевизор, легко услышать кучу аналогичных словосочетаний). Надо ли за них извиняться в тексте?

Конечно, нет! Потому что их надо исправить! Тогда и просить прощения будет не за что.

Кстати, раз уж мы опять заговорили о раздражающих ошибках, то ответьте, пожалуйста, на следующий вопрос: в выражении «извиняюсь за тавтологию» вас больше раздражает
- его неосмысленность (автор концентрирует внимание читателя на ошибке, хотя мог легко её исправить) или
- слово «извиняюсь» (возвратный суффикс в этом глаголе скорее показывает неуважение к читателю, чем искреннее раскаяние)?
А какие ещё выражения вас цепляют?

Хорошего вам понедельника!

Физкультура и математика

У студентов сейчас разгар сессии, но кто-то ещё не очень допущен до экзаменов из-за «ерунды» - отсутствия зачёта по физкультуре. Что делать? Идём к декану (математику).

- Вот, уважаемый, вроде бы по всем предметам успеваете, а на физкультуру редко заходили. Как же так?

- Да я пока лабораторные работы сделаю, пока к конференции доклад подготовлю, пока то, пока сё - вот и время ушло всё.

- Н-да, надо что-то с этим делать. Решите-ка мне задачку! Справитесь - поставлю зачёт своим волевым усилием.

Итак, задачка декана (её недавно предложили в комментариях к заметке о футболе):

На левом краю стометровой резиновой ленты находится студент, желающий получить зачёт. А на правом краю этой ленты ждёт преподаватель физкультуры, готовый поставить студенту зачёт, если тот соизволит подойти. Есть только одна тонкость: как только студент проходит один метр по ленте, она мгновенно растягивается на сто метров.

Другими словами, как только студент проходит метр в сторону преподавателя, лента удлиняется до двухсот метров (поэтому расстояние до заветного зачёта становится равным 198 метров). После этого студент приближается ещё на один метр, а лента опять прибавляет 100 метров к длине. Поэтому студенту надо будет преодолеть 295.5 метров. И так далее.

Вопрос: получит ли студент зачёт, если проявит настойчивость?
(с ленты сходить нельзя)

Уточнения:
- лента растягивается равномерно,
- материал ленты прочный, поэтому она не порвётся, во сколько бы раз её ни растянули,
- студент, желающий получить зачёт, может успеть добраться даже до очень далёкой цели в кратчайшие сроки :)

Студентам желаю легко всё сдать, а семинаристам - подготовленных студентов на экзаменах. И всем хороших выходных!

Железная дорога и один палец

Если проблема легко может быть решена силой воли, то нужна только она - эта самая воля. Пару недель назад я писал о странных недостатках терминала Д в аэропорте Шереметьево:
- закрыты лестницы (как подняться, если большая очередь у лифта? куда бежать при пожаре?),
- неправильно запрограммированы лифты (что создавало большую очередь из желающих подняться).

Это всё мелочи, которые были возможны из-за нехватки ресурсов или желания для производства безупречного результата в локальных задачах. Может быть, дело в отсутствии контроля при сдаче этих этапов... И я вполне могу понять, почему так вышло: при запуске такой большой махины очень трудно уследить за каждым исполнителем. А поскольку у простого пассажира нет, например, прямой возможности перепрограммировать лифт, то вполне может сработать четвёртая власть (хоть это и кажется странным).

Я не ожидал, но сработало всё следующим образом:
1. Несколько блоггеров поделились своими впечатлениями о работе нового терминала.
2. Крупные СМИ оперативно обнаружили эти материалы и перепечатали их фрагменты.
3. Названные проблемы были устранены.

Более того, и с большими проблемами, судя по сообщениям в комментариях и блогах, удаётся бороться:
- заработали электронные терминалы, поэтому меньшему количеству людей надо стоять в очереди к живому человеку,
- увеличилось количество работающих стоек регистрации, что тоже сократило время ожидания.

Другими словами, ситуация налаживается. Возможно, это из-за наших публикаций, а возможно, по каким-то другим причинам (например, погода улучшилась или новые сотрудники лучше освоились на своих местах), но летать снова проще. И это хорошо.

Хочу поблагодарить за оперативность Алекса Экслера (без его поддержки могло ничего не получиться) и журналистов
- интернет-проекта ВГТРК Вести.Ru - они одни из первых подробно осветили проблему, а потом их уже все перепечатали,
- телеканала ТВ Центр - 11 января должен быть выпуск, в создании которого я тоже чуть-чуть поучаствовал (надеюсь, будет интересно),
- Newsweek - они тоже связались со мной, чтобы уточнить некоторые детали «у очевидца».
Были и другие СМИ, отреагировавшие на странную ситуацию. И я думаю, многое стало лучше именно благодаря такой реакции.

Ну раз транспортные проблемы начали решаться так быстро, то есть большое желание узнать ответ на следующий вопрос: :)

Сколько Вы видели сотрудниц касс железной дороги, которые используют более одного пальца при работе на клавиатуре?

Меня это почему-то очень раздражает: освоить относительно быстрый набор текста достаточно просто, но почему-то желающие купить билеты должны в очередях касс ждать, пока все паспортные данные будут вбиты одним пальцем (или даже не пальцем, а ручкой или карандашом). Если эти же данные вводить всеми десятью пальцами, то обслуживание клиентов пойдёт быстрее. Иногда на оформление одного билета уходит более 5 минут (это от момента сообщения всех данных о нужном поезде до получения проездного документа). Конечно, одна из причин такого длительного оформления - медленная база данных или низкая скорость сети. Но и забивание паспортных данных со станцией назначения занимает немало времени - его можно сократить почти бесплатно.

Я понимаю возражение о покупках билетов через интернет. Да, это почти всегда хорошо и удобно, а очереди, скорее всего, не будет вообще. Но у нас же вроде не нулевая безработица сейчас, поэтому можно предложить сотрудникам добровольно повысить свою квалификацию машинистки, воспользовавшись любым из бесплатных тренажёров. И потом уже можно будет поощрять тех, кто хотя бы 150 символов в минуту сможет печатать.

Поэтому повторяю вопрос, чтобы понять, является ли это вообще проблемой:
- много ли Вы видели сотрудниц касс РЖД, умеющих быстро печатать на компьютере?
- приходилось ли когда-нибудь душить позыв предложить кассирше помощь в заполнении всех полей электронной анкеты, чтобы скорее уже бежать на свой поезд? ;)
(оставьте комментарий)

Хороших выходных!

Замуж за иностранца - 2

Пора начинать уже очередной год, правильно? Давайте сделаем что-нибудь неожиданное! Например, можно перекинуться с физических задачек на психологические парадоксы.

Эх, не ту заметку пару месяцев назад я назвал Замуж за иностранца... Там про какую-то математическую логику, а ведь есть настоящая суровая жизнь. Новогоднее общение открыло мне два противоположных взгляда на эту индустрию, которыми я сейчас и поделюсь.

Итак, история первая:

Одна моя знакомая, хорошо знающая пару иностранных языков, трудилась переводчицей в агентстве, работа которого состояла в создании крепких и радостных семей из состоятельных иностранцев и русских девушек, желающих связать с ними свою жизнь. Предлагаю не поднимать сейчас вопросы нравственности, а вглядеться в забавные детали этой работы.

Часто девушки предпочитали не выдумывать свой романтичный ответ на русском языке, который должна была красиво перевести моя знакомая, а просили её «написать что-нибудь хорошее от себя». Не просто так, конечно - они готовы были за это доплатить. Но вникать в сам процесс переписки им вовсе не хотелось. Зачем читать все эти распечатки с размышлениями какого-то там человека, говорящего на непонятном языке?

Порядочность моей знакомой не позволила ей распространяться о смешных случаях в её работе. Впрочем, она подтвердила мои подозрения о том, что забавного в этой индустрии хватает. Но даже без конкретных историй мы знаем уже достаточно, чтобы перейти к взгляду на эту игру глазами второй стороны.

История вторая:

Один европеец рассказал, как он развёлся со своей женой, осознал, что самые лучшие девушки родились в России и Украине, после чего уверенно принял христианство... Далее он начал страстно мечтать о браке с русской или украинской красоткой. Я не знаю, что именно так поменяло его представления о мире, но выглядит всё так, как будто он далеко не один такой.

Что же было дальше? Он нашёл в интернете сайт, где можно переписываться с интересными ему девушками. И даже выбрал одну из них - её фотографии были прекрасны, но это не было важно, потому что она очень интересно отвечала на его письма. Её образованность, чувство юмора, взгляды на жизнь - всё ему в ней нравилось. И она тоже проявляла большой интерес к нему, хорошо чувствуя темы, которые интересны и важны именно ему. А уж её уровень знания его родного языка не позволял сомневаться - надо срочно ехать, пока такую красотку не позвал замуж кто-то другой.

И он приехал в небольшой украинский город, где встретился с ней. И был шокирован тем, что она не может с ним говорить, потому что знает только свой родной язык. А он не знал, что с этим всем делать. Разочарованию не было предела - он попрощался и уехал.

Выглядит это всё как идея для нового сериала «трудности перевода» (не удивлюсь, если уже есть какой-нибудь такой фильм). Но дичь ситуации в том, что это наша реальность:

- Одни имеют много денег, но хотят встретить красивую и интересную девушку.
- Другие хотят много денег, являясь вполне симпатичной, но не самой интересной девушкой. И они готовы «инвестировать» ради своей цели.
- А красивая и интересная девушка подрабатывает переводчицей в какой-то гнилой конторе, потому что не хочет зависеть от дурака, у которого всего лишь есть деньги.

Похоже, я только что рассказал, где принцам искать своих принцесс, но речь не об этом. Важно прочувствовать, как чрезмерная маскировка может всё разрушить. Казалось бы, зачем делать вид, что девушка знает иностранный язык, если она даже не собирается его учить? Сколько можно пытать удачу? Она надеялась своим молодым телом как-то обойти вопрос общения с приехавшим иностранцем? Но если бы ему была нужна продажная женщина, то разве стал бы он тратить столько времени на переписку, разве поехал бы он в такую даль? Я плохо понимаю, на что она рассчитывала. И я знаю очень мало достоверной информации о подобных встречах.

Поэтому вопрос: уважаемые читатели, понимаете ли вы позицию таких барышень? И понимаете ли вы механизм, который может резко изменить предпочтения состоятельных иностранцев в сторону русских и украинских девушек?

Хорошей вам недели!