Есть стандартные моменты, которые трактуются нами почти однозначно. Даже если что-то иногда явно не сформулировано, то мы автоматически принимаем решение, доопределяя ситуацию. И потом не всегда можем чётко вспомнить, что было известно, а что было выдумано для полноты картины.
Есть классический анекдот о том, что человек - не робот:
Жена программиста снаряжает его в магазин: «Купи булку хлеба, а если будут яйца, то возьми десяток». Соответственно, в магазине программист задаёт логичный вопрос: «Скажите пожалуйста, у вас в продаже яйца есть?», на что получает утвердительный ответ. Далее он просит десять булок хлеба.
Но мы с вами отлично знаем, что так не бывает (у большинства :). Люди догадываются о контексте, дополняют недостающие моменты, поэтому проблемы из-за лишней лаконичности и сложного синтаксиса бывают редко.
Приведу в качестве примера задачку, которая мне очень нравится неожиданностью постановки и продуманностью ловушек:
Для ребуса УДАР+УДАР=ДРАКА найти основания систем счисления, в которых он имеет решение.
После этого не требуется объяснять, что одинаковым буквам ребуса соответствуют одинаковые цифры, а разным - разные, не надо говорить, что решением ребуса является такая замены букв на цифры, при котором выражение становится верным. Потому что все это или знают, или сразу догадываются. Заметьте, явно нигде не оговорено, а решить задачку могут многие (желающим я готов подтвердить или опровергнуть правильность их ответа в комментариях или по почте).
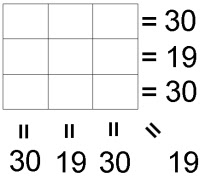
Теперь возвращаемся к исходной теме - к додумыванию неопределённого. В самом начале заметки предложена иллюстрация к задачке с очень простой формулировкой: «Использовать две цифры». Здесь тоже ничего не надо объяснять, потому что и так всё понятно, так ведь?
Казалось бы, человек не должен справляться с этой задачей, потому что нет критерия правильности. Как самого себя проверить, даже если нашёл что-то похожее на ответ? Какие действия применяются к цифрам в ячейках? Компьютеру это не объяснить! Но многие олимпиадники подтвердят, что правильное решение «само выглядит правильным» (у хороших задач, конечно). То есть, если нашёл его, то уже уверен, что как раз оно верное. Поэтому люди с этой задачкой могут справиться.
Получается, что есть какой-то зыбкий субъективный критерий правильности, который компьютеру не объяснить, но десятки тысяч людей во всём мире имеют схожие взгляды на него, поэтому этот спорт существует. И Россия, кстати, традиционно имеет в нём успехи (в прошлый раз китайцы добились наилучшего возможного результата, сместив нашу сборную на второе место, но по количеству золотых медалей российские школьники всех обогнали).
Поэтому я предлагаю подумать об этой задачке, чтобы потом со смыслом проанализировать различные её разборы.
Как обычно бывает с подобными задачами, прошу не публиковать ответы в комментариях хотя бы ближайшие сутки, чтобы случайно не лишить остальных читателей удовольствия от поиска решения.
Первую, думаю, что решил.
ОтветитьУдалитьОснований систем счисления много. Существует итеративная формула.
Mmd, если хотите, то можете проверить, написав свой ответ мне на почту mytribune АТ yandex.ru. Но Ваша формулировака подсказывает мне, что с высокой вероятностью найдены не все решения :)
ОтветитьУдалитьДумается мне, что основание системы счисления - от 2 до бесконечности. В одиночку-то драться неудобно :)
ОтветитьУдалитьAvialaynen, поскольку разных букв в задачке пять, то можно поднять нижнуюю оценку с двух до пяти :)
ОтветитьУдалитьКстати, в этой заметке есть и вторая задачка - про квадрат 3х3 и две цифры.
Я имел в виду, что формулу про удары и драку можно понимать буквально ;)
ОтветитьУдалить8 11 11
ОтветитьУдалить11 - 8
11 8 11
:)
dmitrij, спасибо за интересную версию!
ОтветитьУдалить- - 30
ОтветитьУдалить- 19 -
30 - -
Уважаемый аноним, Ваше решение понятно и интересно, но в нём использованы не две разных цифры, а два разных числа :)
ОтветитьУдалитьА цифр Вы использовали четыре: 0, 1, 3, 9.
Прошу прощения, недопонял. Исправляюсь.
ОтветитьУдалить10 10 10
10 -1 10
10 10 10
Михаил, спасибо за интересную версию! Такой я ещё не видел.
ОтветитьУдалитьИлья, а есть еще варианты решения с двумя цифрами? Мне показалось, что это единственно возможное.
ОтветитьУдалитьМихаил, выше dmitrij предложил вариант с единицей и восьмёркой. Я в своё время придумал с единицей и девяткой. Недостаток обоих этих решений - не все клетки заполнены. Но это требование в условии не оговорено.
ОтветитьУдалитьXXX
ОтветитьУдалитьXIX
XXX
Похоже, дожали задачку.
ОтветитьУдалитьArthaus, согласитесь, что достаточно придумать это решение, чтобы отказаться от поиска других вариантов! Потому что оно выглядит правильным :)
кажется, что конкретный пример к ударам это 8126
ОтветитьУдалитьУважаемый аноним, в этой задаче спрашивается, в каких системах счисления существует решение, а не хотя бы один пример :)
ОтветитьУдалить12 1/2 - 11/2 - 12
ОтветитьУдалить11/2 - 1 - 12 1/2
12 - 12 1/2 - 11/2
Не очень удачная форма записи, здесь фигурируют числа 12,5; 5,5; 12; 1
Оригинально! :)
ОтветитьУдалитьA A A
ОтветитьУдалитьA FF A
A A A
в хексе по модулю 0x100 :)
Тоже оригинально вышло. Не увядает задачка-то :)
ОтветитьУдалитьПервую задачу я сначала поняла так, что в каждой клеточке должна стоять цифра. Но тогда сумма 30 быть не может. Тогда я сделала вывод, что из цифр можно составлять числа, но у меня снова получилось, что решения нет. Наконец, я решила оставить одну из клеток пустой, и у меня получилось:
ОтветитьУдалить11-8-11
8-_-11
11-11-8
Была ещё мысль про знаки действий, но я сочла, что, во-первых, это наверняка бы оговаривалось, во-вторых, тогда задача стала бы совсем уж ерундовой.
В числовом ребусе я ничего такого не заметила. Обычная позиционнная система счисления, одинаковые буквы -- одинаковые цифры, разные -- разные, ни одно многозначное число не начинается с нуля, знаки "+" и "=" имеют своё обычное значение. Имелось в виду, что, что-нибудь другое? Если нет, то где же здесь "неожиданность" и "ловушки"?
Ребус имеет решение при основании семь, а так же при основаниях 10, 14, 18 и так далее (то есть таких, которые делятся на два, но не на четыре и при этом не меньше 10). Если хотите, могу прислать решение.
> Первую задачу я сначала поняла так, что в каждой клеточке должна стоять цифра. Но тогда сумма 30 быть не может.
УдалитьЭто не совсем так. Выше в комментариях предложено решение, в котором в каждой клеточке стоит ровно одна цифра, а всего использовано только две различных цифры.
> В числовом ребусе я ничего такого не заметила
Здорово, что Вам легко даются такие задачи!
> Если хотите, могу прислать решение.
Только если Вы сами бы хотели, чтобы я его посмотрел. Ответ Вы назвали верный (кстати, семёрку многие не замечают, что лишний раз говорит о Вашей высокой внимательности), поэтому, скорее всего, решение тоже имеете хорошее.
1) По обычным правилам игры цифры или числа в такого рода задачах складываются. Решение, на которое Вы дали ссылку, я видела и заценила, но моя собственная мысль, какое именно из обычных правил нарушил автор, пошла другим путём. А вот решение юзера Ilya K мне непонятно вовсе.
Удалить2) Просто я решала числовые ребусы и раньше. И даже сама их сочиняла. Так что мучительно постигать правила игры не пришлось. Кстати, задача с ребусом сложнее задачи с квадратом в том смысле, что тут требуется проверить все возможности, а не просто обнаружить какой-нибудь вариант, но при этом мне не пришлось мучительно гадать, в чём же автор нарушил правила игры.
3) Узнать, как оно понравится Вам, хотела бы. Стоит ли выкладывать его здесь в комментах -- не уверена. Тема старая, но Вы и в старые завлекаете новых юзеров. ;) Можно обсудить моё решение по почте?
> А вот решение юзера Ilya K мне непонятно вовсе.
УдалитьОн предлагает работать в шестнадцетеричной системе (там A = 10 в десятичной, а FF = 255 в десятичной), но при этом работать по модулю 256. Т.е. любая операция (а нас тут интересует только сложение), дополняется взятием остатка от деления на 256. Например, А + FF + A = (10 + 255 + 10) mod 256 = 19.
> Можно обсудить моё решение по почте?
Да, конечно, пишите на адрес mytribune АТ yandex.ru.
Значит хексом Илья называет 16-ричную систему счисления? А почему тогда "по модулю 0x100", а не просто "по модулю 100"? Это описка или что-нибудь значит?
УдалитьДа, это стандартное название.
УдалитьА префикс "0x" традиционно означает, что следующее за ним следует понимать, как шестнадцатеричное число (см. http://en.wikipedia.org/wiki/0x).
Письмо Ваше получил, в ближайшее время отвечу.
Теперь понятно. Илья, наверное, программист с профессиональной деформацией личности. :)
УдалитьНо хочу всё-таки уточнить, что никакой ихний инглиш я ни хрена не понимаю, в связи с чем мне пришлось заменить en на ru.
З.Ы. Кстати, с пустыми клетками я нашла для квадрата ещё два решения (не считая отражений относительно диагонали).
ОтветитьУдалить19-_-11
_-_-19
11-19-_
18-1-11
1-_-18
11-18-1
Спасибо за новые варианты решения этой задачки!
УдалитьИзвините, слово "ещё" здесь лишнее. Опять я чукча-писатель... Не "ещё два", а просто два, причём один из них есть в коммменте другого юзера.
УдалитьЗ.Ы. Из комментов поняла, что второе моё решение Вам тоже было известно. Но у меня появилась ещё одна мысль...
УдалитьЕсли предположить, что неизвестные числа записаны в другой системе счисления, чем известные, или что имеется в виду арифметика остатков, задача становится совсем ерундовой: достаточно взять двоичную систему, где цифр и так всего две, или вычеты по модулю два. Например:
Удалить1000-1010-1100
1010-1-1000
1100-1000-1010 (в двоичной системе)
0-0-0
0-1-0
0-0-0 (по модулю два)
А вот если допустить, что все числа, включая неизвестные, записаны в одной и той же НСС, но с неизвестным основанием, найти решение не так просто, но можно. У меня получилось, что тогда возможны четыре решения. Впрочем, я пока ещё жду ответа на предыдущее письмо. ;)
Приношу извинения, было много неотложных дел.
УдалитьПоказывайте свои четыре решения, заинтриговали :)
Ну вот, мне пришёлв голову ещё один вариант. Если не указано иного, система десятичная, но цифры можно ставить и нижним (или и нижним, и верхним) индексом. Ведь если писать от руки на бумаге, дополнительных символов для этого не надо.
ОтветитьУдалитьНапример так (я не знаю, сработает ли здесь тэг нижнего индекса и на всякий случай обозначу его круглыми скобкам):
11-111(2)-12
111(2)-1-11
12-11-111(2)
Может всё-таки объясните, ЧТО имел в виду автор? А то я просто теряюсь в догадках!
Мне кажется, самое естественное решение - использование римских цифр. Собственно, придумав это решение, человек обычно чувствует, что именно его и ожидает автор, т.к. оно не предполагает каких-либо действий (например, использование сложения в остальных вариантах естественно (т.к. есть прямая ассоциация с магическими квадратами), но обойтись без него было бы гораздо естественнее), использует ровно две цифры. Короче, выглядит хорошо. В этом и плюс, и минус недостаточно формализованных задачек.
УдалитьЯ не понимаю, откуда Вы взяли, что "придумав это решение, человек обычно чувствует, что именно его ожидает автор". Потому что оно "не предполагает каких-либо действий"? Но откуда Вы взяли, что автор ожидал именно этого? "Обойтись без сложения было бы гораздо естественнее"? А почему Вы считате, что это естественнее? Мне вот самым естественным показалось решение с индексами. То, что указанный Вами вариант Вам больше всего нравится, ещё не значит, что автор предполагал именно его.
УдалитьУ меня были случаи, когда я находила решение лучше авторского, во всяком случае, со своей точки зрения. Вот пример: http://mi3ch.livejournal.com/1984076.html?thread=106787148#t106787148
В заметке специально были сделаны реверансы на тему «задачи недоопределены, поэтому понять их условие и проверить правильность решения может только человек». У нас нет жёстких правил, но есть ощущения. И у меня ощущение, что решение с римскими цифрами самое изящное. Но остальные мне тоже нравятся :)
УдалитьСпасибо за ссылку на изящное решение задачи про блогера и букву «c»!